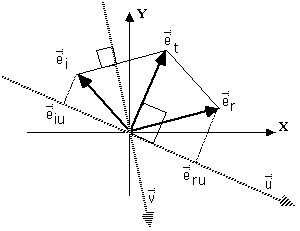
Expression des composantes tangentielles des champs
On se place en \(Z = 0\) (qui désigne le plan de séparation des deux milieux) et on désigne par les lettres minuscules les valeurs en \(Z = 0\) des vecteurs obtenus par la projection dans ce plan de chacun de ces champs (i.e. leurs composantes tangentielles).
Dans le milieu \((1)\) :
\(\vec E_{1 ~ \mathrm{tangentiel}} = \vec e_i + \vec e_r\)
\(\Rightarrow ~~~~ \vec e_i + \vec e_r = \vec e_t\)
Dans le milieu \((2)\) :
\(\vec E_{2 ~ \mathrm{tangentiel}} = \vec e_t\)
Cette relation de continuité est représentée sur le schéma ci-contre, dans le plan \((X, Y)\) séparant les deux milieux.
Sur ce schéma :
\(\vec u\) désigne le vecteur unitaire orthogonal à \(\vec e_t\)
\(\vec v\) désigne le vecteur unitaire orthogonal à \(\vec e_r\)