Orbitales Moléculaires d'une molécule diatomique hétéronucléaire

Partie

On suppose que les deux noyaux de deux atomes de type différents sont maintenus à une distance fixe (ce qui revient à appliquer l'approximation de Born-Oppenheimer). Pour simplifier l'analyse, considérons donc deux OA de même type provenant de chacun des deux atomes et formant une liaison.

On notera :

atome \(\phi\) 1 : orbitale 1, d'énergie \(\alpha\) 1

atome \(\phi\) 2 : orbitale 2, d'énergie \(\alpha\) 2

Les énergies \(\alpha\) 1 et \(\alpha\) 2 sont différentes.

Les orbitales moléculaires s'écrivent selon :

Ψ = c 1 . ϕ 1 + c 2 . ϕ 2 %PSI=c_{1}.%phi_{1}+c_{2}.%phi_{2}

et sont solution de l'équation de Schrödinger : H\(\Psi\) = E\(\Psi\) qui s'écrit encore :

< Ψ | H | Ψ > = E . < Ψ | Ψ > "<"%PSI"|"H"|"%PSI">" =E."<"%PSI"|"%PSI">"

But général : donner les expressions analytiques des orbitales et de l'énergie.

On définit :

α i = < ϕ i | H | ϕ i > β i , j = < ϕ i | H | ϕ j > S i , j = < ϕ i | ϕ i > %alpha_{i} = "<"%phi_{i}"|"H"|"%phi_{i}">" newline %beta_{i,j} = "<"%phi_{i}"|"H"|"%phi_{j}">" newline S_{i,j} = "<"%phi_{i}"|"%phi_{i}">"

Avec

- \(\alpha\) i les intégrales coulombiennes, elles représentent en première approximation l'énergie d'un électron occupant l'orbitale \(\Phi\) idans l'atome i isolé. \(\alpha\) i est négative et sa valeur absolue doit croître avec l'électronégativité de A

-\(\beta\) ij les intégrales de résonnance, Sa valeur absolue donne une mesure de la force de la liaison entre les deux atomes. C'est une fonction croissante de l'intégrale de recouvrement S12.

- Sij les intégrales de recouvrement.

Question

Ecrire la condition sur les énergies et les coefficients.

Intégrons l'expression de l'orbitale moléculaire dans l'équation de Schrödinger :

< c 1 ϕ 1 + c 2 ϕ 2 | H | c 1 ϕ 1 + c 2 ϕ 2 > = E . < c 1 ϕ 1 + c 2 ϕ 2 | c 1 ϕ 1 + c 2 ϕ 2 > "<"c_{1}%phi_{1}+c_{2}%phi_{2}"|"H"|"c_{1}%phi_{1}+c_{2}%phi_{2}">" =E."<"c_{1}%phi_{1}+c_{2}%phi_{2}"|"c_{1}%phi_{1}+c_{2}%phi_{2}">"

Lorsque i=j, on obtient : Sii = 1car les orbitales atomiques sont normées, soit S11 = S12 = 1. De plus, comme ici les deux atomes, et les deux orbitales, 1 et 2 sont de même type, on a \(\beta\) 12=\(\beta\) 21 que l'on notera \(\beta\).

Solution détaillée

On obtient :

< c 1 ϕ 1 | H | c 1 ϕ 1 > + < c 2 ϕ 2 | H | c 2 ϕ 2 > + 2. < c 1 ϕ 1 | H | c 2 ϕ 2 > = E . ( < c 1 ϕ 1 | c 1 ϕ 1 > + < c 2 ϕ 2 | c 2 ϕ 2 > + 2. < c 1 ϕ 1 | c 2 ϕ 2 > ) c 1 2 . α + c 2 2 . α + 2 c 1 c 2 . β = E ( c 1 2 + c 2 2 + 2 c 1 c 2 S ) "<"c_{1}%phi_{1}"|"H"|"c_{1}%phi_{1}">" + "<"c_{2}%phi_{2}"|"H"|"c_{2}%phi_{2}">" + 2."<"c_{1}%phi_{1}"|"H"|"c_{2}%phi_{2}">" newline " ="E.("<"c_{1}%phi_{1}"|"c_{1}%phi_{1}">"+"<"c_{2}%phi_{2}"|"c_{2}%phi_{2}">"+2."<"c_{1}%phi_{1}"|"c_{2}%phi_{2}">") newline newline c_{1}^{2}.%alpha + c_{2}^{2}.%alpha +2c_{1}c_{2}.%beta=E(c_{1}^{2}+c_{2}^{2}+2c_{1}c_{2}S)

Question

Finalement, on obtient la condition suivante sur les énergies et les coefficients c1 et c2 :

c 1 2 . α 1 + c 2 2 . α 2 + 2 c 1 c 2 . β = E ( c 1 2 + c 2 2 + 2 c 1 c 2 S ) c_{1}^{2}.%alpha_1 + c_{2}^{2}.%alpha_2 +2c_{1}c_{2}.%beta=E(c_{1}^{2}+c_{2}^{2}+2c_{1}c_{2}S)

Une nouvelle fois, cette équation est généralisée et donc valable pour toutes les orbitales moléculaires, c'est-à-dire pour tout les couples {E,(c1,c2)}. Dans la suite de la démonstration, il faudra donc garder en mémoire quelle solution on recherche.

Question : Les inconnues de cette équation sont c1, c2 et E. Déterminer les expressions des énergies.

Pour cela, on s'appuiera sur la méthode variationnelle. Pour minimiser E, on différencie et on annule les dérivées partielles :

∂ E ∂ c 1 = ∂ E ∂ c 2 = 0 {partial E} over {partial c_{1}} = {partial E} over {partial c_{2}}=0
Solution détaillée

On obtient le système d'équation suivant :

c 1 ( α 1 − E ) + c 2 ( β − E . S ) = 0 c 1 ( β − E . S ) + c 2 ( α 2 − E ) = 0 c_{1}(%alpha_1-E) +c_{2}(%beta-E.S) =0 newline c_{1}(%beta-E.S) +c_{2}(%alpha_2-E)=0

qui n'accepte de solutions non triviales que si son déterminant associé est nul :

| α 1 − E β − E . S β − E . S α 2 − E | = 0 left lline matrix {%alpha_1-E#%beta-E.S##%beta-E.S#%alpha_2-E} right rline =0

qui se développe selon :

( α 1 − E ) ( α 2 − E ) − ( β − E . S ) 2 = 0 (%alpha_1-E)(%alpha_2-E)-(%beta-E.S)^2=0

les solutions s'écrivent alors:

E 1 = α 1 + α 2 − 2 β S + Δ 2 ( 1 − S 2 ) E 2 = α 1 + α 2 − 2 β S − Δ 2 ( 1 − S 2 ) avec Δ = ( 2 β S − α 1 − α 2 ) 2 − 4 ( 1 − S 2 ) ( α 1 α 2 − β 2 ) E_{1}={ alignc {%alpha_1+%alpha_2 -2%beta S + sqrt{%DELTA}} over {2(1-S^2)}} newline E_{2}={ alignc {%alpha_1+%alpha_2 -2%beta S - sqrt{%DELTA}} over {2(1-S^2)}} newline "avec" newline %DELTA=(2%beta S- %alpha_1 - %alpha_2)^2-4(1-S^2)(%alpha_1 %alpha_2-%beta^2)

Les solutions ne sont pas triviales, appliquons quelques simplifications afin d'obtenir des solutions plus simples.

Les deux atomes sont de types différents. L'énergie de leur orbitale (même si elles sont de types identique) sont également différentes. Posons \(\alpha\) 1<\(\alpha\) 2.

La méthode variationnelle tend à maximiser la participation de l'orbitale atomique de plus basse énergie dans l'écriture de l'orbitale moléculaire de plus basse énergie. En première approximation, le plus bas niveau énergétique moléculaire sera plus négatif que la plus négative des orbitales atomiques, dans notre cas \(\alpha\) 1. On obtiendra la tendance inverse pour l'orbitale atomique de plus haute énergie.

Ainsi, l'approximation qui mène à la résolution la plus simple consiste à considérer que les solutions sont presque indépendantes

E 1 ≈ α 1 E 2 ≈ α 2 E_{1} approx %alpha_1 newline E_{2} approx %alpha_2

Dans ce cadre, E1 sera plus négative que \(\alpha\) 1et E2 sera légèrement moins négative que \(\alpha\) 2. E1 sera donc le niveau associé à l'orbitale liante et E2 sera associé à l'orbitale antiliante.

Considérons E1, la condition provenant du développement du déterminant donne :

α 1 − E 1 = ( β − E 1 S ) 2 ( α 2 − E 1 ) ≈ ( β − α 1 S ) 2 ( α 2 − α 1 ) %alpha_1-E_1={alignc (%beta-E_1 S)^2 over (%alpha_2-E_1)} approx {alignc (%beta- %alpha_1 S)^2 over (%alpha_2-%alpha_1)}

Considérons E2, la condition provenant du développement du déterminant donne :

α 2 − E 2 = ( β − E 2 S ) 2 ( α 1 − E 2 ) ≈ ( β − α 2 S ) 2 ( α 1 − α 2 ) %alpha_2-E_2={alignc (%beta-E_2 S)^2 over (%alpha_1-E_2)} approx {alignc (%beta- %alpha_2 S)^2 over (%alpha_1-%alpha_2)}

Les solutions énergétiques s'écrivent :

E 1 ≈ α 1 + ( β − α 1 S ) 2 ( α 1 − α 2 ) E 2 ≈ α 2 − ( β − α 2 S ) 2 ( α 1 − α 2 ) E_1 approx %alpha_1 + {alignc (%beta- %alpha_1 S)^2 over (%alpha_1-%alpha_2)} newline newline E_2 approx %alpha_2 - {alignc (%beta- %alpha_2 S)^2 over (%alpha_1-%alpha_2)}

Question

Écrire les expressions des deux orbitales moléculaires.

Afin de trouver les orbitales associées à chacun de ces niveaux énergétique, il faut ré-injecter chacune des valeurs d'énergie dans le système d'équations. Une condition supplémentaire, la condition de normation, sera nécessaire pour déterminer complètement le jeu de coefficients de chacune des orbitales.

Solution détaillée

Avec E1, On obtient le système d'équation séculaire :

{ c 1 [ α 1 − ( α 1 + ( β − α 1 S ) 2 / ( α 1 − α 2 ) ) ] + c 2 ( β − α 1 S ) = 0 c 1 ( β − α 1 S ) + c 2 ( α 2 − α 1 ) = 0 left lbrace matrix { c_1 [%alpha_1 - (%alpha_1+(%beta-%alpha_1 S)^2 / (%alpha_1 - %alpha_2))] + c_2 (%beta - %alpha_1 S)=0 ## c_1(%beta - %alpha_1 S) + c_2 (%alpha_2 - %alpha_1) = 0} right none
− c 1 ( β − α 1 S ) / ( α 1 − α 2 ) + C 2 = 0 -c_1(%beta - %alpha_1 S) / (%alpha_1 - %alpha_2) + C_2 =0

La condition de normation nous permet d'obtenir le coefficient assurant le fait que la solution est normée. On la notera N1. La répétition de ce formalisme pour E2 nous permet d'obtenir les coefficients pour l'orbitale de plus haute énergie.

Les solutions s'écrivent :

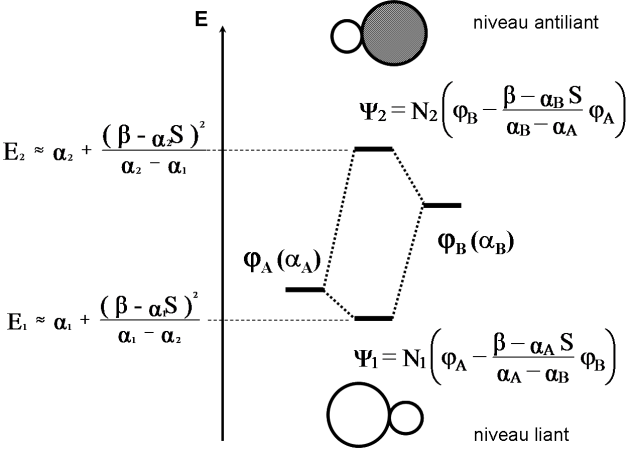
Ψ 1 = N 1 ( ϕ 1 − β − α 1 S α 1 − α 2 ϕ 2 ) Ψ 2 = N 2 ( ϕ 2 − β − α 2 S α 2 − α 1 ϕ 1 ) %PSI_1 = N_1 left ( %phi_1- {%beta - %alpha_1 S} over { %alpha_1 - %alpha_2} %phi_2 right ) newline newline %PSI_2 = N_2 left ( %phi_2- {%beta - %alpha_2 S} over { %alpha_2 - %alpha_1} %phi_1 right )

En résumant tout sur un schéma énergétique :