Généralisation pour N électrons
On pourrait généraliser à \(\textrm N\) électrons ; la fonction d'onde serait alors le produit de \(\textrm N\) spin-orbitales. Ce résultat est caractéristique des particules indépendantes sans interactions mutuelles pour lesquelles il est légitime de trouver que l'énergie totale est simplement la somme d'énergies individuelles.
On obtient là un modèle très simple, dans lequel il suffit de choisir un jeu de spin orbitales pour décrire les électrons de l'atome et de bâtir le produit de ces fonction pour obtenir l'état quantique qui décrit mathématiquement le nuage électronique.
Ce modèle permet même s'affranchir du langage rigoureux et subtil de la mécanique quantique pour décrire les états du nuage électronique des atomes. On peut opter pour une description plus symbolique et visuelle et transformer un modèle théorique en quelque chose de plus facilement manipulable :
Ainsi, pour décrire un état dans lequel on utilise \(\textrm N\) spin-orbitales, on peut dessiner le spectre des niveaux d'énergie des orbitales atomiques et placer les électrons avec leur spin sur les niveaux correspondant aux spin-orbitales utilisées.
En peuplant ainsi les niveaux, on construit symboliquement une fonction d'onde polyélectronique, sans avoir à se pencher sur les expressions mathématiques. Un niveau occupé par un électron symbolise alors une orbitale qui intervient dans la fonction d'onde ; la flèche que l'on porte sur le niveau pour représenter le spin de l'électron décrit la fonction de spin que l'on attache à cette orbitale pour former la spin-orbitale occupée.
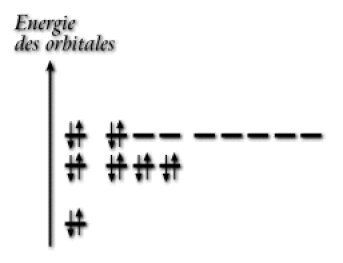
Spectre énergétique des orbitales
De même, on peut utiliser le schéma des cases quantiques vu dans le chapitre précédent. Dans ce schéma, on place les électrons dans les cases avec le spin adéquat pour former l'état électronique de l'atome.
On dit alors que l'on peuple les orbitales avec des électrons de spin \(\alpha\) ou \(\beta\) .
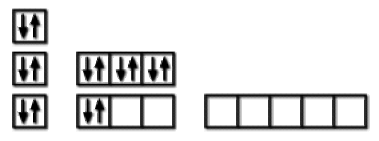
Schéma de cases quantiques
Cependant, même si on néglige les interactions entre électrons, la fonction d'onde ne peut se présenter sous une forme aussi simple ; elle n'est pas convenable. Il faut en effet, pour des particules quantiques, tenir compte du principe d'indétermination.