Définition
Soit \(f\) une application de \(I\) dans \(\mathbb R\). Intuitivement \(f\) est continue en \(x_0\) si \(f(x)\) est voisin de \(f(x_0)\) quand \(x\) est voisin de \(x_0\), ou si \(f(x)- f(x_0)\) est petit quand \(x - x_0\) est petit.
Définition : Fonction continue en un point
On dit que \(f\) est continue en \(x_0\) si l'une ou l'autre des propriétés équivalentes 1. ou 2. est vérifiée.
Pour tout voisinage \(\mathcal V\) de \(f(x_0)\), il existe un voisinage \(\mathcal U\) de \(x_0\) tel que, si \(x\) appartient à \(\mathcal U\cap I\), alors \(f(x)\) appartient à \(\mathcal V\).
Quel que soit \(\epsilon>0\), il existe \(\eta>0\) tel que, si \(x\) appartient à \(I\) et vérifie \(\vert x- x_0\vert <\eta\) , on ait \(\vert f(x)-f(x_0)\vert<\epsilon\).
La propriété 2. se traduit en langage formalisé :
\(\displaystyle{\forall\epsilon>0,\exists\eta>0,\forall x\in I\textrm{ }(\vert x-x_0\vert<\eta\Rightarrow\vert f(x)-f(x_0)\vert<\epsilon)}\)
Il est bien évident que \(\eta\) dépend a priori de \(f\), de \(\epsilon\) et de \(x_0\).
Par ailleurs les inégalités sont indifféremment larges ou strictes.
Méthode :
Lorsqu'on étudie directement la continuité d'une fonction en un point, on cherche à établir au voisinage du point une inégalité du type :
\(\displaystyle{\vert f(x)-f(x_0)\vert\leq k\vert x-x_0\vert}\),
\(k\) étant un réel dépendant de \(x_0\).
Exemple :
a. La fonction \(x\mapsto ax\) est continue en tout point \(x_0\in\mathbb R\)
On peut choisir \(\eta\) quelconque si \(a=0\) et \(\displaystyle{\eta=\frac{\epsilon}{\vert a\vert}\textrm{ si }a\neq 0}\).
Illustration graphique :
\(f :x\mapsto2x\)
Vous pouvez visualiser les points de la courbe représentant la fonction sur la figure suivante. Pour cela vous devez d'abord cliquer sur le bouton "Déplacer" puis déplacer le point à l'aide des flèches droite et gauche du clavier.
b. La fonction sinus est continue en tout point \(x_0\in\mathbb R\).
On peut choisir \(\eta=\epsilon\) d'après l'inégalité
\(\displaystyle{\vert\textrm{sin }x-\textrm{sin }x_0\vert =2\Big|\textrm{sin }\Big(\frac{x-x_0}{2}\Big)\textrm{ cos }\Big(\frac{x+x_0}{2}\Big)\Big|\le2\Big|\textrm{sin }\Big(\frac{x-x_0}{2}\Big)\le\vert x-x_0\vert}\)
Illustration graphique :
\(f :x\mapsto\textrm{sin}(x)\)
Vous pouvez visualiser les points de la courbe représentant la fonction sur la figure suivante. Pour cela vous devez d'abord cliquer sur le bouton "Déplacer" puis déplacer le point à l'aide des flèches droite et gauche du clavier.
c. La fonction carré est continue en tout point \(x_0\in\mathbb R\).
Illustration graphique :
\(f :x\mapsto x^2\)
Vous pouvez visualiser les points de la courbe représentant la fonction sur la figure suivante. Pour cela vous devez d'abord cliquer sur le bouton "Déplacer" puis déplacer le point à l'aide des flèches droite et gauche du clavier.
On écrit \(\vert x^2-x_{0}^2\vert=\vert x+x_0\vert\vert x-x_0\vert\), or \(\vert x+x_0\vert\) est borné au voisinage de \(x_0\), par exemple, si on se restreint à l'intervalle \([x_0-1,x_0+1]\cap I\), on a alors \(\vert x+x_0\vert\le2\vert x_0\vert+1\);
d'où, en prenant \(\displaystyle{\eta=\textrm{min }\bigg(1,\frac{\epsilon}{2\vert x_0\vert+1}\bigg)}\), on obtient \(\vert x^2-x_0^2\vert<\epsilon\).
On remarque que, dans ce dernier cas, la recherche d'une relation liant \(\eta\) et \(\epsilon\) fait intervenir \(x_0\) et que, en conséquence, \(\eta\) dépend de \(x_0\) ce qui n'était pas le cas pour les autres exemples.
d. La fonction f définie par
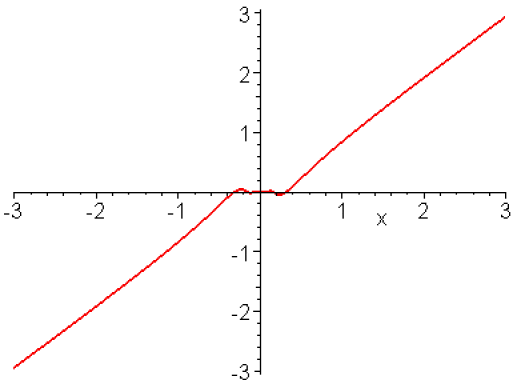
\(\displaystyle{\forall x\ne0 :f(x)=x^2\textrm{sin}\frac{1}{x},f(0)=0}\)
est continue en 0.
Illustration graphique :
graphe pour \(-3<x<3\)
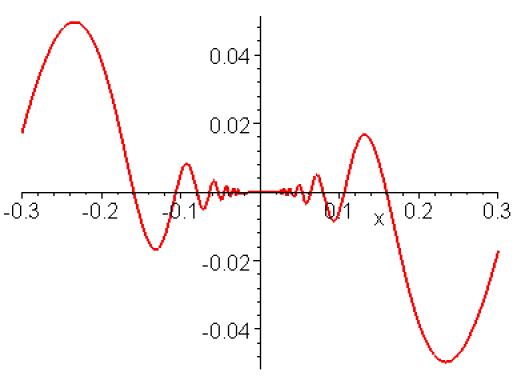
graphe pour \(-0.3<x<0.3\)
Animation "zoom" :
Le premier écran montre les graphes des fonctions \(\displaystyle{x\mapsto x^2\textrm{ sin}\bigg(\frac{1}{x}\bigg)}\) (en rouge), \(\displaystyle{x\mapsto-x^2}\) et \(\displaystyle{x\mapsto x^2}\) dans une fenêtre où \(x\) varie de \(-1\) à \(+1\) et \(y\) varie de \(-1\) à \(+1\). L'animation consiste à "zoomer", c'est à dire à réduire l'intervalle affiché de façon à voir de plus en plus gros les détails, jusqu'à arriver à une fenêtre de largeur 0,1.
Proposition :
Si \(f\) est continue en \(x_0\) alors \(f\) est bornée au voisinage de \(x_0\).
La traduction formelle de cette proposition est la suivante :
\(\exists M\in\mathbb R,\exists\alpha>0,\forall x\in I\textrm{ }(\vert x-x_0\vert<\alpha\Rightarrow\vert f(x)\vert\le M)\).
Preuve :
Le choix d'un \(\epsilon=1\) par exemple permet de conclure. En effet :
On prend \(\epsilon=1\); il existe \(\alpha>0\) tel que \(\vert x-x_0\vert <\alpha\) entraîne \(\vert f(x)-f(x_0)\vert<1\), soit \(f(x_0)-1<f(x)<f(x_0)+1\),
d'où : \(\vert f(x)\vert<\vert f(x_0)\vert +1\).