Exercice 4
Durée : 10 mn
Note maximale : 10
Question
Soit \(f_n\) la fonction définie, pour tout entier naturel \(n\), par :
\(\displaystyle{\forall x\in\left[0,\frac{n}{n+1}\right]~f_n(x)=nx^n,~~\forall x\in\left]\frac{n}{n+1},1\right]~f_n(x)=n^{n+1}(1-x)^n}\).
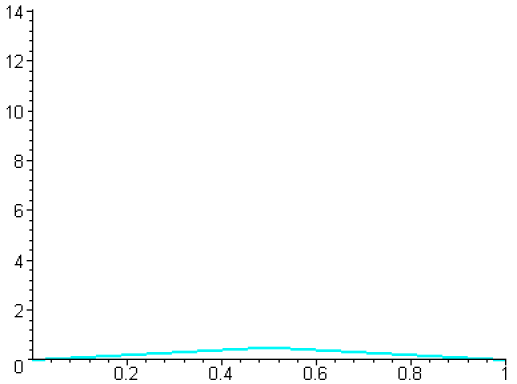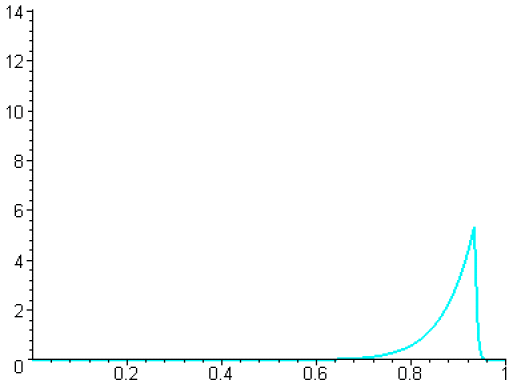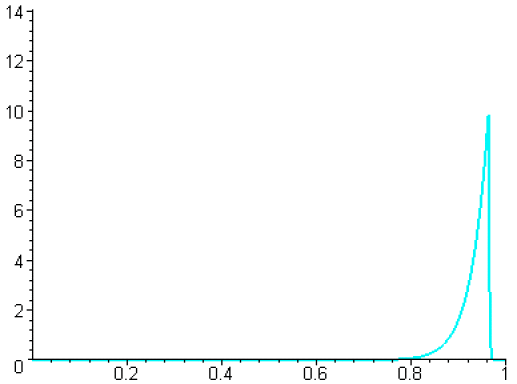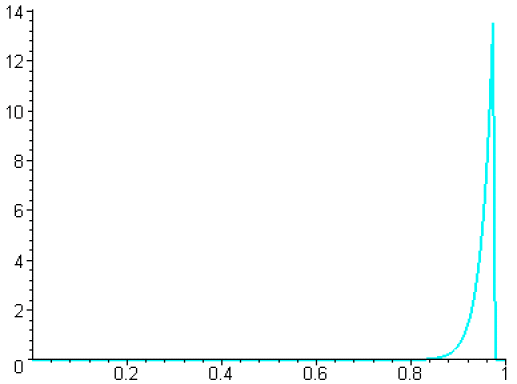
Montrer que \(f_n\) est continue en tout point de l'intervalle \([0,1]\) et tracer son graphe.
Etudier la suite \(\displaystyle{\left(f_n\left(\frac{n}{n+1}\right)\right)}\).
Etudier, pour \(x\in[0,1]\), la suite \((f_n(x))\). Le résultat est-il contradictoire avec le résultat précédent ?
Solution
1. Sur les intervalles \(\displaystyle{\left[0,\frac{n}{n+1}\right]}\) et \(\displaystyle{\left]\frac{n}{n+1},1\right]}\) la fonction \(f_n\) est polynomiale et donc continue. On a \(\displaystyle{f_n\left(\frac{n}{n+1}\right)=n\left(\frac{n}{n+1}\right)^n=\lim_{n\rightarrow\left(\frac{n}{n+1}\right)^-}f_n(x)}\), la fonction est donc également continue au point \(\displaystyle{\frac{n}{n+1}}\).
La fonction \(f_n\) est croissante sur \(\displaystyle{\left[0,\frac{n}{n+1}\right]}\) et décroissante sur \(\displaystyle{\left]\frac{n}{n+1},1\right]}\).
[2 points]
Voici le graphe pour les valeurs 1,...,10 de \(n\).
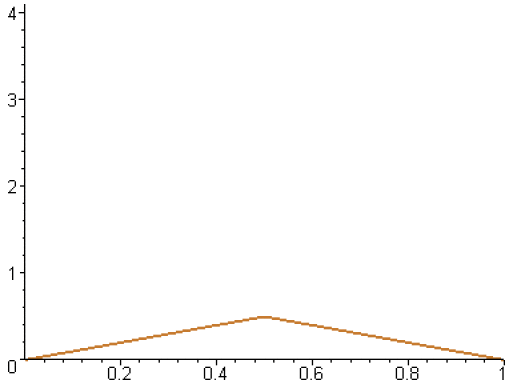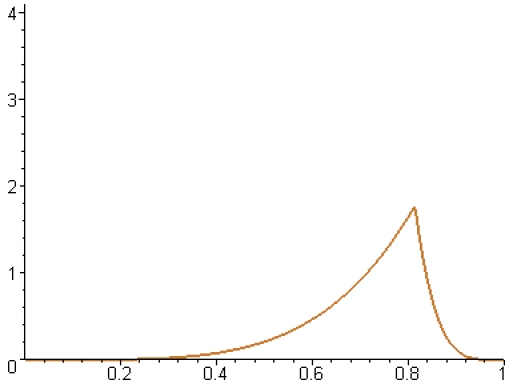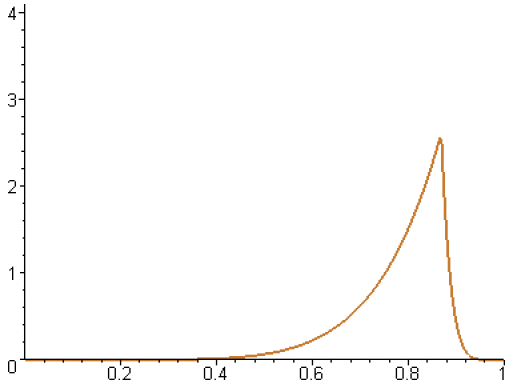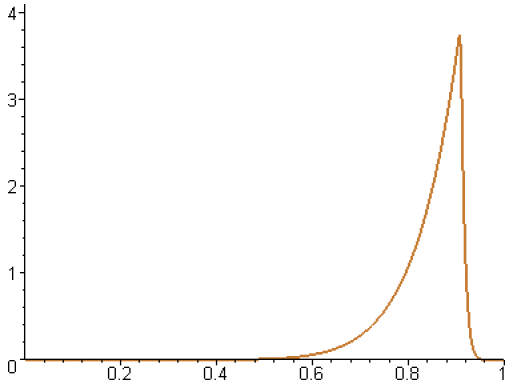
On écrit \(\displaystyle{f_n\left(\frac{n}{n+1}\right)=\frac{n}{\left(1+\frac{1}{n}\right)^n}}\), or, quand \(n\) tend vers \(+\infty\), \(\displaystyle{\lim_{n\rightarrow+\infty}\left(1+\frac{1}{n}\right)^n=e}\) (limite classique qu'on peut retrouver en étudiant le logarithme du terme général de la suite).
On en déduit : \(\displaystyle{f_n\left(\frac{n}{n+1}\right)\rightarrow+\infty}\) quand \(n\rightarrow+\infty\) .
[2 points]
3. On a : pour \(x=1,\forall n\ge0~f_n(1)=0\) et pour \(x=0,\forall n\ge0~f_n(0)=0\). Soit \(x\) un réel fixé vérifiant : \(0<x<1\), il existe un rang \(n_0\) tel que, pour \(n\ge n_0\), en ait \(\displaystyle{x<\frac{n}{n+1}}\), d'où \(f_n(x)=nx^n\). On étudie alors :
\(\displaystyle{\ln f_n(x)=\ln n+n\ln x=n\ln x\left(1+\frac{\ln n}{n\ln x}\right)}\);
comme \(\displaystyle{\lim_{n\rightarrow+\infty}\frac{\ln n}{n\ln x}=0}\) et \(\ln x<0\), \(\ln f_n(x)\) tend vers moins l'infini et \(f_n(x)\) tend vers \(0\).
[3 points]
Ce résultat n'est pas en contradiction avec le résultat précédent : ici on étudie une suite \((f_n(x))\) avec \(x\) fixé tandis qu'on étudiait précédemment une suite \((f_n(x_n))\) où \((x_n)\) est une suite de limite \(1\).
[3 points]
Voici le graphe pour les valeurs 1,...,40 de \(n\).