Étude de fonction (1)
Partie
On considère la fonction \(f\) définie sur l'intervalle \(I =]0, \frac{\pi}{2}]\)par \(f(x) = \frac{1}{x\sin x}.\)
Question
Montrer que \(f\) est continue sur \(I\) puis qu'elle établit une bijection de \(I\) sur l'intervalle \(J = [\frac{2}{\pi},+\infty[.\)
Aide simple
La fonction \(x\mapsto \sin x\)est strictement croissante sur l'intervalle \(]0,\frac{\pi}{2}].\)
Aide à la lecture
Quelque soit le réel \(x\) appartenant à l'intervalle \(]0,\frac{\pi}{2}],\) le réel \(x\sin x\)n'est pas nul : ceci justifie la définition de \(f.\)
Aide méthodologique
Une fonction \(f\) définie sur \(I\) est toujours une surjection sur \(f(I).\)
L'image d'un intervalle par une fonction continue est un intervalle.
Une fonction \(f\) continue sur un intervalle est injective si et seulement si elle est strictement monotone.
On peut appliquer alors le théorème dit des fonctions réciproques.
Solution détaillée
La fonction \(x\mapsto \sin x\)est continue sur \(I=]0,\frac{\pi}{2}]\)comme produit de fonctions continues sur \(I\) et ne s'annule pas sur cet intervalle.
Donc la fonction \(f :x\mapsto\frac{1}{x\sin x}\)est continue sur \(I=]0,\frac{\pi}{2}].\)
Il suffit alors de vérifier qu'elle est strictement monotone sur \(I\) pour en conclure qu'elle établit une bijection de \(I\) sur l'intervalle \(f(I).\) (Voir la proposition sur la caractérisation de l'injectivité d'une fonction continue sur un intervalle :
Soit \(f\) une fonction continue sur un intervalle.
1. Si \(f\) est strictement monotone, alors elle est injective.
2. Si \(f\) est injective, alors elle est strictement monotone.).
Sur \(I=]0,\frac{\pi}{2}],\) les fonctions \(x\mapsto x\)et \(x\mapsto \sin x\)sont strictement positives et strictement croissantes donc leur produit aussi, d'où \(f\) est strictement décroissante sur \(I=]0,\frac{\pi}{2}].\)
Donc la fonction \(f\) est une bijection de l'intervalle \(I\) sur \(f(I).\)
Or d'après la proposition sur la nature de l'image d'un intervalle par une fonction continue strictement monotone, on a \(f(I) =[f(\frac{\pi}{2}),\displaystyle \lim_{x\mapsto 0}f(x)[.\)
Comme la fonction \(x\mapsto\sin x\)tend vers \(0\) par valeurs positives lorsque \(x\) tend vers \(0\) par valeurs positives, on en déduit que la fonction \(f\) tend vers \(+\infty\)quand \(x\) tend vers \(0.\)
Donc \(f(I) = [\frac{2}{\pi},+\infty[.\)
Proposition : nature de l'image d'un intervalle par une fonction continue strictement monotone
Soit \(f\) une fonction continue et strictement monotone sur un intervalle \(I.\)
Si \(a\) et \(b\) désignent les extrémités de l'intervalle \(I\) (c'est-à-dire \(a\) ou \(b\) sont des réels ou sont les symboles \(-\infty\)ou \(+\infty)\) alors les extrémités de l'intervalle \(f(I)\)sont \(\displaystyle \lim_{x\rightarrow a}f(x)\)et \(\displaystyle \lim_{x\rightarrow b}f(x),\) (ces limites pouvant être elles-mêmes infinies).
De plus les intervalles \(I\) et \(f(I)\)sont de même nature : fermés, ouverts, ou semi-ouverts.
Question
Soit\(f^{-1}\) la fonction réciproque de \(f.\)
Montrer que \(f^{-1}\)est dérivable sur \(J\) et calculer sa dérivée au point \(\frac{2}{\pi}.\)
Aide simple
Théorème des fonctions réciproques :
Soit \(f\) une fonction continue strictement monotone sur un intervalle \(I.\) Alors
1) \(f(I)\) est un intervalle \(J\) de même nature que \(I\) (fermé, ouvert ou semi ouvert) et ses extrémités sont les limites de\( f\) aux extrémités de \(I.\)
2) La fonction \(f\) admet une fonction réciproque définie sur \(J = f(I)\); plus précisément, \(f\) définit une bijection de l'intervalle \(I\) sur l'intervalle \(J,\) donc il existe une fonction notée \(f^{-1}~\textrm{de}~J\) dans \(I,\) telle que
\(\begin{array} {|l|}\hline x \in I\\ y = f(x) \\ \hline \end{array}~~\Leftrightarrow~~\begin{array} {|l|}\hline y \in J\\ x = f^{-1}(y) \\ \hline \end{array}\)
3) La fonction réciproque \(f^{-1}\)est continue et strictement monotone sur \(J,\) de même sens de monotonie que \(f.\)
4) De plus, si \(f\) est dérivable en un point \(x_0\) de \(I\) et si \(f'(x_0)\)est non nul, \(f^{-1}\)est dérivable au point \(y_0 = f(x_0)~\textrm{et}~(f^{-1})'(y_0) = \frac{1}{f'(x_0)} = \frac{1}{f'(f^{-1}(y_0))}.\)
Solution détaillée
Pour montrer que \(f^{-1}\)est dérivable sur \(J,\) il suffit d'après le théorème des fonctions réciproques de vérifier que \(f\) est dérivable sur \(I\) et que sa dérivée ne s'annule pas sur \(I.\)
La fonction \(f\) est dérivable comme produit et quotient de fonctions dérivables ne s'annulant pas sur \(I.\)
Sa dérivée est la fonction \(f' :x\mapsto\frac{-\sin x - x\cos x}{x^2\sin^2x}.\)
Sur l'intervalle \(I=]0,\frac{\pi}{2}],\) le réel \((-\sin x)\)est strictement négatif et le réel \((-x\cos x)\)est négatif ou nul, donc \(f'\) est strictement négatif. (On retrouve ainsi le fait que la fonction \(f\) est strictement décroissante.)
La fonction \(f'\) ne s'annule donc pas sur \(I=]0,\frac{\pi}{2}].\)
Donc la fonction \(f^{-1}\)est dérivable sur l'intervalle \(J=[\frac{2}{\pi},+\infty[.\)
De plus sa dérivée au point \(\frac{2}{\pi}\)est \(\frac{1}{f'(f^{-1}(\frac{2}{\pi}))}=\frac{1}{f'(\frac{\pi}{2})}.\) On trouve :
\((f^{-1})'(\frac{2}{\pi})=-\frac{4}{\pi^2}\)
Remarque : on ne peut pas expliciter la fonction\(f^{-1}\) mais on sait qu'elle est continue strictement décroissante et dérivable sur l'intervalle \(J=[\frac{2}{\pi},+\infty[.\)
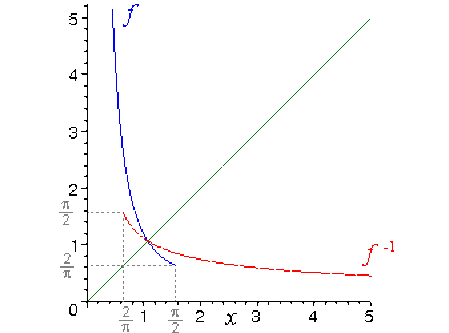
Représentations graphiques des fonctions \(f\) et \(f^{-1}\)