Étude de fonction (3)
Partie
Soit \(f\) la fonction numérique définie pour tout nombre réel \(x\) par \(f(x) = x|x|.\)
Question
Montrer que la fonction \(f\) est continue sur \(\mathbb R.\)
Aide simple
Attention la fonction \(x\mapsto|x|\)n'est pas dérivable en \(0,\) donc pour décider de la dérivabilité de \(f\) en \(0,\) revenir à la définition de dérivée en un point.
Théorème des fonctions réciproques :
Soit \(f\) une fonction continue strictement monotone sur un intervalle \(I.\) Alors
1) \(f(I)\) est un intervalle \(J\) de même nature que \(I\) (fermé, ouvert ou semi ouvert) et ses extrémités sont les limites de\( f\) aux extrémités de \(I.\)
2) La fonction \(f\) admet une fonction réciproque définie sur \(J = f(I)\); plus précisément, \(f\) définit une bijection de l'intervalle \(I\) sur l'intervalle \(J,\) donc il existe une fonction notée \(f^{-1}~\textrm{de}~J\) dans \(I,\) telle que
\(\begin{array} {|l|}\hline x \in I\\ y = f(x) \\ \hline \end{array}~~\Leftrightarrow~~\begin{array} {|l|}\hline y \in J\\ x = f^{-1}(y) \\ \hline \end{array}\)
3) La fonction réciproque \(f^{-1}\)est continue et strictement monotone sur \(J,\) de même sens de monotonie que \(f.\)
4) De plus, si \(f\) est dérivable en un point \(x_0\) de \(I\) et si \(f'(x_0)\)est non nul, \(f^{-1}\)est dérivable au point \(y_0 = f(x_0)~\textrm{et}~(f^{-1})'(y_0) = \frac{1}{f'(x_0)} = \frac{1}{f'(f^{-1}(y_0))}.\)
Aide à la lecture
On dit qu'une fonction numérique \(f\) continue sur un intervalle \(I\) admet une fonction réciproque lorsque \(f\) est une bijection de \(I\) sur l'intervalle \(J=f(I),\) la bijection réciproque étant définie sur \(J.\)
Aide méthodologique
Une fonction numérique \(f\) continue sur un intervalle \(I\) est une bijection de \(I\) sur l'intervalle \(J=f(I),\) si et seulement si elle est strictement monotone.
Pour montrer qu'une fonction \(f\) est dérivable en un point, soit on se sert des propriétés sur la somme, produit ou composée de fonctions dérivables, soit on revient à la définition de la dérivée en un point \(a\) en cherchant si le rapport \(\frac{f(x)-f(a)}{x-a}\)a une limite finie.
Solution détaillée
La fonction \(f\) est continue sur \(\mathbb R\) comme produit des deux fonctions continues\(x\rightarrow x\) et \(x\rightarrow|x|.\)
Question
Montrer que la fonction \(f\) admet une fonction réciproque, notée \(f^{-1},\) dont on donnera l'intervalle de définition \(J\) et les propriétés immédiates.
Solution détaillée
On sait qu'une fonction continue sur un intervalle \(I\) admet une fonction réciproque si et seulement si elle est strictement monotone sur \(I.\)
Si \(x\) et \(y\) vérifient \(0<x<y,\) alors \(f(x)=x^2\)et \(f(y)=y^2\)donc \(0<f(x)<f(y).\)
Si \(x\) et \(y\) vérifient \(x<y<0,\) alors \(f(x)=-x^2,\) \(f(y)=-y^2\)et \(x^2>y^2\);
dans ce cas \(f(x)<f(y)<0.\)
Comme \(f(0)=0,\) on en déduit que \(f\) est strictement croissante sur \(\mathbb R.\)
La fonction \(f\) étant continue et strictement croissante sur \(\mathbb R\) admet donc, d'après le théorème des fonctions réciproques , une fonction réciproque \(f^{-1}\)définie sur \(f(\mathbb R).\)
On cherche \(f(\mathbb R)\): on sait que \(f(\mathbb R)=]\displaystyle \lim_{x\rightarrow-\infty}f(x), \displaystyle \lim_{x\rightarrow+\infty}f(x)[.\)
Quand \(x\) tend vers \(+\infty,\) \(f(x)\)tend vers \(+\infty,\)
et quand \(x\) tend vers \(-\infty,\) \(f(x)\) tend vers \(-\infty.\)
Donc \(J=f(\mathbb R) = \mathbb R.\)
La fonction \(f^{-1}\)est donc définie continue et strictement croissante sur \(\mathbb R.\)
Question
La fonction \(f\) est-elle dérivable sur \(\mathbb R\) ?
Que peut-on dire à priori sur la dérivabilité de la fonction \(f^{-1}\)?
Solution détaillée
La fonction \(x\rightarrow|x|\)n'est pas dérivable en \(0\) mais est dérivable en tout réel différent de \(0\) ; la fonction \(x\rightarrow x\)est dérivable sur \(\mathbb R\) donc la fonction \(f\) est dérivable sur \(\mathbb R^*\)comme produit de fonctions dérivables ; comme de plus \(\displaystyle \lim_{x\rightarrow 0}\frac{f(x)-f(0)}{x}=\displaystyle \lim_{x\rightarrow 0}\frac{x|x|}{x} = 0,\) on en déduit que \(f\) est dérivable en \(0\) donc \(f\) est dérivable sur \(\mathbb R.\)
Donc à priori, d'après le théorème des fonctions réciproques , la fonction \(f^{-1}\)est dérivable en tout point \(y\) image par \(f\) d'un point \(x\) tel que \(f'(x)\neq0.\)
Or si \(x\) est strictement positif \(f(x) = x^2\)et \(f'(x)=2x,\) si \(x\) est strictement négatif
\(f(x)=-x^2\)et \(f'(x)=-2x,\) et pour \(x=0\)on a \(f'(0)=0.\)
Donc la dérivée de la fonction \(f\) ne s'annule qu'en \(x=0\)et comme \(y=f(0)=0,\) on en déduit que \(f^{-1}\)n'est dérivable à priori que sur \(\mathbb R^*.\)
Question
Expliciter la fonction \(f^{-1}.\)
Cette fonction est-elle dérivable sur \(J\) ?
Solution détaillée
Dans ce cas particulier, on peut déterminer \(f^{-1}\):
en effet si \(x\) est positif, \(y=f(x)\)l'est aussi, et : \((y=x^2)\Leftrightarrow(x=\sqrt{y}).\)
et si \(x\) est négatif, \(y=f(x)\)l'est aussi, et : \((y=-x^2)\Leftrightarrow(x=-\sqrt{-y}).\)
Donc \(f^{-1}\)est la fonction \(\begin{cases} x\mapsto\sqrt{x}~~~~\textrm{pour}~~x>0\\x\mapsto-\sqrt{-x}~~~~\textrm{pour}~~x<0\\0\mapsto 0\end{cases}\)
Pour savoir si \(f^{-1}\)est dérivable au point \(0,\) on considère l'expression \(\frac{f^{-1}(x)-f^{-1}(0)}{x}\):
Quand \(x\) tend vers \(0\) par valeurs positives, \(\frac{f^{-1}(x)-f^{-1}(0)}{x} = \frac{\sqrt x}{x}\)n'a pas de limite finie (ni l'expression \(\frac{f^{-1}(x)-f^{-1}(0)}{x} = \frac{-\sqrt {-x}}{x}\)quand \(x\) tend vers \(0\) par valeurs négatives).
Donc \(f^{-1}\)n'est pas dérivable en \(0.\)
Conclusion : la fonction \(f\) est une fonction continue strictement croissante et dérivable sur \(\mathbb R,\) tandis que la fonction \(f^{-1}\)est une fonction continue strictement croissante sur \(\mathbb R,\) mais n'est pas dérivable sur \(\mathbb R,\) elle est cependant dérivable sur \(\mathbb R^*.\)
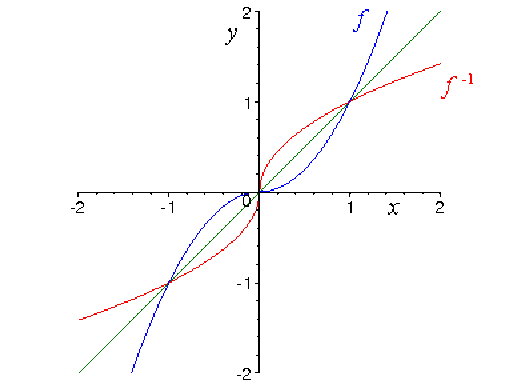
Soit \(C_f\)la représentation graphique de \(f\) et \(C_{f^{-1}}\)celle de \(f^{-1},\) dans un repère orthonormé ;
\(C_f\)et \(C_{f^{-1}}\)sont symétriques par rapport à la première bissectrice.
On remarque que la tangente à \(C_f\)au point d'abscisse \(0\) est horizontale tandis que la tangente à \(C_{f^{-1}}\)au même point est verticale.
Représentations graphiques des fonctions \(f\) et \(f^{-1}.\)