Variations et représentation graphique
Le domaine de définition de la fonction \(\ln\)est l'intervalle \(]0, \infty[.\)
Elle est continue et strictement croissante car sa dérivée est positive.
Comportement aux bornes :
\(\boxed{\displaystyle \lim_{x \rightarrow \infty}\ln x = +\infty}\)
En effet soit \(A > 0~~\exists n_0 \in \mathbb N ^*~~n_0\ln 2 > A\)car \(\ln 2 > 0\)et \(\mathbb R\) archimédien.
Alors \(x > 2^{n_0} \Rightarrow \ln x > \ln 2^{n_0} \Rightarrow \ln x > n_0 \ln 2\)et finalement \(\ln x > A\)
La première implication est due à la croissance du logarithme, la deuxième à une des relations précédentes et la troisième à la transitivité de la relation d'ordre dans \(\mathbb R.\)
\(\boxed{\displaystyle \lim_{x \rightarrow 0^+}\ln x = - \infty}\)
car \(\ln x = - \ln(1/x),~~x \rightarrow 0^+ \Leftrightarrow 1/x \rightarrow +\infty\)
\(\boxed{\displaystyle \lim_{x \rightarrow + \infty}\frac{(\ln x)}{x} = 0}\)
Démonstration :
Tout d'abord \(\forall x \geq 1~~\ln x \leq x\)
La fonction \(h\) définie par \(h(x) = x - \ln x\)est dérivable sur \([1, +\infty[,~~h'(x) = 1 - \frac{1}{x}\) donc \(\forall x \in [1, +\infty[~~h'(x) \geq 0,\) la fonction \(h\) est croissante, \(\forall x \in [1, +\infty[~~h(x) \geq h(1),~~h(1) = 1 \Rightarrow h(x) \geq 0\)
Alors \(\forall x \geq 1~~0 \leq \frac{\ln x}{x} = \frac{2\ln\sqrt{x}}{(\sqrt{x})^2}\leq \frac{2}{\sqrt x}.\)
Ces inégalités permettent de terminer la démonstration.
En appliquant le théorème des fonctions continues monotones, on conclut que la fonction logarithme népérien établit une bijection de \(]0, +\infty[\)sur \(\mathbb R.\)
En particulier le réel \(1\) possède un unique antécédent noté \(e,\) \(\ln e = 1.\)
Dans un repère orthonormé on obtient le graphe suivant :
\(\begin{array}{|c | c c c|}\hline x & 0 & & +\infty \\ \hline & & & +\infty \\ \ln x & & \nearrow & \\ & -\infty & & \\ \hline \end{array}\)
\(\color{red} x \mapsto \ln x\)
\(\color{blue} x \mapsto x - 1\)
\(\color{magenta} x \mapsto \frac{1}{e}x\)
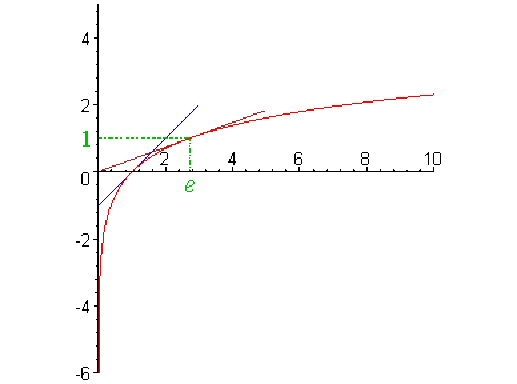
On observe que :
la droite d'équation \(x = 0\)est une asymptote,
le graphe présente une branche parabolique de direction horizontale car \(\displaystyle \lim_{x \rightarrow +\infty}\frac{(\ln x)}{x} = 0,\)
la droite, d'équation \(y = x - 1,\) est tangente au graphe au point \((1, 0),\)
la droite, d'équation \(y = \frac{1}{e}x,\) est tangente au graphe au point \((e, 1).\)