Définition
Soient\( \mathcal A \textrm{ et }\mathcal B\) deux matrices. On suppose que le nombre de colonnes de \(\mathcal A\) est égal au nombre de lignes de \(\mathcal B\). Dans ces conditions, on va pouvoir définir le produit \(\mathcal{AB}\).
On va formaliser ces hypothèses pour donner la définition. Soit donc \(n, p\) et \(q\) trois entiers supérieurs ou égaux à \(1\).
Définition :
soit \(\mathcal A=(a_{i,j})\) une matrice à \(n\) lignes et \(p\) colonnes ; soit \(\mathcal B=(b_{k,l})\) une matrice à \(p\) lignes et \(q\) colonnes. Alors\( \mathcal{AB}\) est la matrice à n lignes et q colonnes dont le terme général \(c_{i,l}\) est donné par la formule \(\displaystyle{c_{i,l}=\sum_{j=1}^{j=p}a_{i,j}b_{j,l}}\).
Illustration
On peut écrire le coefficient \(c_{i,l}\) de façon plus développée, à savoir :
\(\displaystyle{c_{i,l}=a_{i,1}b_{1,l}+a_{i,2}b_{2,l}+\cdots+a_{i,j}b_{j,l}+\cdots+a_{i,p}b_{p,l}}\).
Sous cette forme, on comprend mieux la contrainte imposée sur les nombres de colonnes et de lignes de \(\mathcal A \textrm{ et }\mathcal B\) respectivement.
Donc, pour avoir l'élément de la i-ième ligne l-ième colonne de \(\mathcal{AB}\), on prend la i-ième ligne de la matrice qui est à gauche c'est-à-dire \(\mathcal A\), la l-ième colonne de la matrice qui est à droite c'est-à-dire \(\mathcal B\) ; on fait le produit du premier élément de la ligne par le premier élément de la colonne, puis du deuxième élément de la ligne par le deuxième élément de la colonne et ainsi de suite jusqu'au produit du \(p\)-ième élément de la ligne par le \(p\)-ième élément de la colonne et l'on fait la somme de tous ces produits.
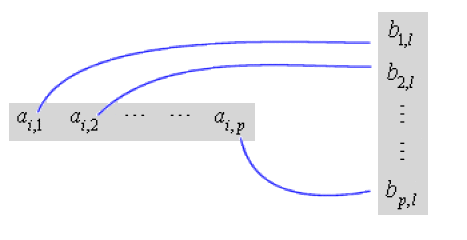
Illustration : on va prendre \(p=5\). La situation précédente devient donc :
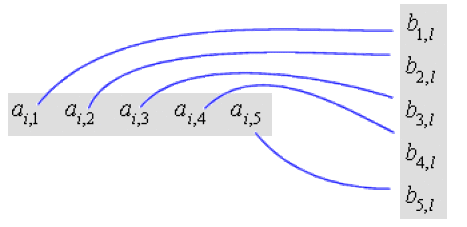
alors \(\displaystyle{c_{i,l}=a_{i,1}b_{1,l}+a_{i,2}b_{2,l}+a_{i,3}b_{3,l}+a_{i,4}b_{4,l}+a_{i,5}b_{5,l}}\).
Le calcul s'effectue de la façon suivante :