Rang de matrices

L'étude des transformations élémentaires a conduit au résultat suivant :

Soit \(p\) et \(n\) des entiers supérieurs ou égaux à \(1\) et \(\mathcal M\) une matrice de \(\mathcal M_{n,p}(\mathbf K)\), non nulle.

Alors, il existe un entier \(r\), supérieur ou égal à \(1\), et inférieur ou égal à \(p\) et à \(n\), et deux matrices \(\mathcal P\) et \(\mathcal Q\) tels que :

• les matrices\( \mathcal P\) et \(\mathcal Q\) appartiennent respectivement à \(\mathcal M_n(\mathbf K)\) et \(\mathcal M_p(\mathbf K)\) et sont des produits de matrices élémentaires,

• on a l'égalité : \(\mathcal M=\mathcal P\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,p-r}\\\mathcal O_{n-r,r}&\mathcal O_{n-r,p-r}\end{array}\right)\mathcal Q\).

De plus, comme les matrices élémentaires sont inversibles, les matrices \(\mathcal P\) et\( \mathcal Q\) le sont aussi.

En utilisant le langage vu dans le paragraphe précédent, cela signifie que la matrice \(\mathcal M\) est équivalente à la matrice \(\left(\begin{array}{cccccc}\mathcal I_r&\mathcal O_{r,p-r}\\\mathcal O_{n-r,r}&\mathcal O_{n-r,p-r}\end{array}\right)\) . Cela donne alors, d'après le résultat du paragraphe précédent, des résultats intéressants sur \(r\).

• Interprétation de \(r\) : C'est le rang de la matrice \(\mathcal M\)

• Unicité de \(r\) : L'algorithme qui permet de trouver \(r, \mathcal P, \mathcal Q\) satisfaisant aux conditions indiquées donne une construction effective de\( r, \mathcal P\),et \(\mathcal Q\) mais ne permet pas de savoir si l'entier \(r\) trouvé est unique ou pas. L'interprétation précédente donne une réponse à cette question. L'entier \(r\) est unique c'est le rang de la matrice \(\mathcal M\). Cela permet de donner l'énoncé plus complet suivant :

Dans la troisième partie, on avait déjà trouvé un résultat analogue, avec la différence suivante :

la méthode est plus théorique et ne donne pas un calcul effectif de \(\mathcal P\) et \(\mathcal Q\) alors qu'ici, on sait que ce sont des produits de matrices élémentaires qui peuvent être déterminées par un algorithme.

Cela amène à une autre méthode pratique pour déterminer le rang d'une matrice.

La matrice qui a les mêmes colonnes que \(\mathcal M\) sauf éventuellement la \(j\)-ième qui est égale à \(\mathcal C_j+\lambda\mathcal C_i\) est la matrice \(\mathcal M\mathcal T_{i,j}(\lambda)\) .

Soient\( i\) un entier compris entre \(1\) et \(p\) et \(\lambda\) un élément non nul de \(\mathbf K\).

On considère la matrice carrée d'ordre \(p,\mathcal D_i(\lambda)\)

La matrice qui a les mêmes colonnes que \(\mathcal M\) sauf éventuellement la \(i\)-ième qui est égale à est \(\lambda\mathcal C_i\) est la matrice \(\mathcal M\mathcal D_i(\lambda)\).

On rappelle que les matrices élémentaires sont définies de la façon suivante :

Soit \(n\) un entier supérieur ou égal à \(2\). Soient deux entiers distincts \(i\) et \(j\), compris entre \(1\) et \(n\), et \(\lambda\) un élément de \(\mathbf K\).

• On définit la matrice \(\mathcal T_{i,j}(\lambda)\in\mathcal M_n(\mathbf K)\) par

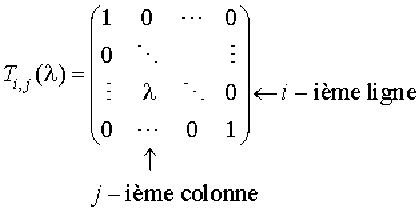
Les éléments de la diagonale principale sont tous égaux à \(1,\lambda\) se trouve à la \(i\)-ième ligne et \(j\)-ième colonne et tous les autres éléments sont nuls.

• Soit \(\lambda\) un élément non nul de \(\mathbf K\).

  On définit la matrice diagonale \(\mathcal D_i(\lambda)\in\mathcal M_n(\mathbf K)\) par :

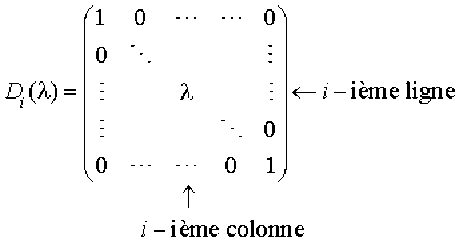
\(\lambda\) se trouve à la\( i\)-ième ligne et \(i\)-ième colonne, tous les autres éléments de la diagonale principale sont égaux à \(1\).

Soient i et j deux entiers distincts compris entre \(1\) et \(p\). On considère la matrice d'ordre \(p\).

On considère la matrice \(\Delta_{i,j}\) d'ordre \(p\).

Alors la matrice obtenue à partir de \(\mathcal M\) en échangeant les colonnes \(i\) et\( j\) de \(\mathcal M\) est égale à \(\mathcal M\Delta_{i,j}\).

On rappelle que les matrices \(\Delta_{i,j}\) sont définies de la façon suivante :

Soit k un entier supérieur ou égal à \(2\). Soient\( i\) et\( j\) deux entiers distincts compris entre \(1\) et \(k\).

La matrice carrée d'ordre \(k,\Delta_{i,j}\), est la matrice dont

• Les éléments de la diagonale principale sont tous égaux à \(1\) sauf le \(i\)-ième et le \(j\)-ième, qui sont nuls

• L'élément de la i-ième ligne, j-ième colonne est égal à \(1\), ainsi que celui de \(j\)-ième ligne, \(i\)-ième colonne.

• Tous les autres éléments sont nuls.

Donc

C'est une matrice symétrique et elle vérifie, pour tout \(i\) et \(j\) entiers compris entre \(1\) et \(k\), l'égalité : \(\Delta_{i,j}=\delta_{j,i}\).

De plus on a démontré la formule \(\Delta_{i,j}=\mathcal T_{i,j}(1)\mathcal T_{j,i}(-1)\mathcal T_{i,j}(1)\mathcal D_i(-1)\).

Les matrices élémentaires intervenant dans cette formule ont le même ordre que \(\Delta_{i,j}\).

Transformations sur les lignes

Soient \(i\) et \(j\) deux entiers distincts compris entre \(1\) et \(n\) et\( \lambda\) un élément quelconque de \(\mathbf K\). On considère la matrice carrée d'ordre \(n,\mathcal T_{i,j}(\lambda)\) .

La matrice qui a les mêmes lignes que \(\mathcal M\) sauf éventuellement la\( i\)-ième qui est égale à \(\mathcal L_i+\lambda\mathcal L_j\) est la matrice \(\mathcal T_{i,j}(\lambda)\mathcal M\).

Soient \(i\) un entier compris entre \(1\) et \(n,\lambda\) un élément non nul de \(\mathbf K\). On considère la matrice carrée d'ordre \(n,\mathcal D_i(\lambda)\) .

La matrice qui a les mêmes lignes que \(\mathcal M\) sauf éventuellement la \(i\)-ième qui est égale à est est \(\lambda\mathcal L_i\) la matrice\( \mathcal D_i(\lambda)\mathcal M\).

Échange de lignes

Soient\( i\) et \(j\) deux entiers distincts compris entre \(1\) et \(n\) et la matrice

\(\Delta_{i,j}=\mathcal T_{i,j}(1)\mathcal T_{j,i}(-1)\mathcal T_{i,j}(1)\mathcal D_i(-1)\) ,

où les matrices élémentaires intervenant sont toutes carrées d'ordre \(n\).

Alors la matrice obtenue à partir de \(\mathcal M\) en échangeant les lignes \(i\) et \(j\) de \(\mathcal M\) est égale à \(\Delta_{i,j}\mathcal M\).