Déterminants : définition, propriétés, calcul

• Calcul de \(D_1\) (2 points)

On peut développer \(D_1\) suivant la première colonne :

\(D_1=\left|\begin{array}{ccc}3&5&-5\\2&-5&4\\1&2&1\end{array}\right|=(-1)^{1+1}\times3\left|\begin{array}{cc}-5&4\\2&1\end{array}\right|+(-1)^{2+1}\times2\left|\begin{array}{cc}5&-5\\2&1\end{array}\right|+(-1)^{3+1}\left|\begin{array}{cc}5&-5\\-5&4\end{array}\right|\)

\(D_1=3(-5-8)-2(5+10)+(20-25)=-39-30-5=-74\)

On peut également utiliser la règle de Sarrus :

On réécrit les deux premières colonnes à droite de la troisième colonne.

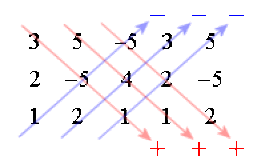
\(D_1\) est égal à la somme des produits des éléments reliés par une flèche, affectés du signe + si la flèche est parallèle à la diagonale principale, affectés du signe si la flèche est parallèle à l'autre diagonale :

\(D_1=3\times(-5)\times1+5\times4\times1+(-5)\times2\times2-(-5)(-5)\times1-3\times4\times2-5\times2\times1\)

\(D_1=-15+20-20-25-24-10=-74\)

• Calcul de \(D_2\) (4 points)

\(D_2=\left|\begin{array}{ccc}1+i&1-2i&1+i\\1-2i&1+i&1+i\\1+i&1+i&1-2i\end{array}\right|\)

On retranche successivement la colonne 1 à la colonne 2 et à la colonne 3 \((C_2\leftarrow C_2-C_1, C_3\leftarrow C_3-C_1)\). Ces transformations ne modifient pas \(D_2\) et permettent d'obtenir d'une part un zéro sur chacune des colonnes 2 et 3, d'autre part une factorisation de \(D_2\).

\(D_2=\left|\begin{array}{ccc}1+i&-3i&0\\1-2i&3i&3i\\1+i&0&-3i\end{array}\right|\)

Un déterminant est linéaire par rapport à chacune de ses colonnes, donc

\(D_2=(3i)^2\left|\begin{array}{ccc}1+i&-1&0\\1-2i&1&1\\1+i&0&-1\end{array}\right|\)

On ajoute la ligne 3 à la ligne 2 \((L_2\leftarrow L_2+L_3)\) :

\(D_2=-9\left|\begin{array}{ccc}1+i&-1&0\\2-i&1&0\\1+i&0&-1\end{array}\right|\)

Puis on développe suivant la troisième colonne :

\(D_2=(-9)(-1)(-1)^{3+3}\left|\begin{array}{cc}1+i&-1\\2-i&1\end{array}\right|=9(1+i+2-i)=27\)

• Calcul de \(D_3\) (4 points)

\(D_3=\left|\begin{array}{ccccc}1&-2&1&3&4\\1&-1&0&2&4\\2&1&3&1&2\\-1&0&1&1&3\\0&1&-1&1&5\end{array}\right|\)

Afin d'avoir quatre zéros sur la première colonne on fait successivement les transformations suivantes : \(L_2\leftarrow L_2-L_1 ;L_3\leftarrow L_3-2L_1 ;L_4\leftarrow L_4+L_1\) (on retranche à la ligne 2 la ligne 1, on retranche à la ligne 3 deux fois la ligne 1, on ajoute la ligne 1 à la ligne 4)

\(D_3=\left|\begin{array}{ccccc}1&-2&1&3&4\\0&1&-1&-1&0\\0&5&1&-5&-5\\0&-2&2&4&7\\0&1&-1&1&5\end{array}\right|\)

On développe suivant la première colonne :

\(D_3=\left|\begin{array}{cccc}1&-1&-1&0\\5&1&-5&-6\\-2&2&4&7\\1&-1&1&5\end{array}\right|\)

Afin d'avoir trois zéros sur la première ligne, on fait successivement les transformations suivantes : \(C_2\leftarrow C_2+C_1 ;C_3\leftarrow C_3+C_1\) (ajout de la colonne 1 à la colonne 2 et à la colonne 3)

\(D_3=\left|\begin{array}{cccc}1&0&0&0\\5&6&0&-6\\-2&0&2&7\\1&0&2&5\end{array}\right|\)

On développe suivant la première ligne :

\(D_3=\left|\begin{array}{ccc}6&0&-6\\0&2&7\\0&2&5\end{array}\right|=6\left|\begin{array}{cc}2&7\\2&5\end{array}\right|=6(10-14)=-24\)