Définition d'une série entière
Définition :
Une série entière est une série de fonctions \(\sum{f_n}\) où, pour tout entier \(n\), \(f_n\) est de la forme : \(f_n : C \rightarrow C\) \(z\mapsto a_nz^n\), (\(a_n\in C\)).
Une série entière est donc une série de fonctions puissances (power series en anglais) et la suite \((S_n)\) des fonctions sommes partielles associées est une suite de fonctions polynomiales :
\(S_n: C\rightarrow C\) \(z\mapsto S_n(z)=\displaystyle{\sum_{k=0}^n}a_kz^k\).
Les nombres \(a_n\) sont les coefficients de la série entière. Une série entière est entièrement déterminée par la donnée de la suite \((a_n)\)de ses coefficients.
Règle : Notation
On note \(\sum a_nz^n\) (\(\displaystyle{\sum_{n\geq n_0}}a_nz^n\) quand la suite \((a_n)\) des coefficients est définie pour \(n\geq n_0\)). Ce symbolisme est ambigu, car il désigne à la fois :
la série entière c'est-à-dire la série de fonctions,
pour \(z\) fixé, la série numérique à termes complexes \(\sum a_nz^n\)
On distinguera série de fonctions et série à termes complexes en parlant dans le premier cas de la série entière \(\sum a_nz^n\), et dans le second de la série \(\sum a_nz^n\).
Règle : Notation : disque ouvert, fermé, cercle
On notera, pour un réel :\(C(0,r)\):
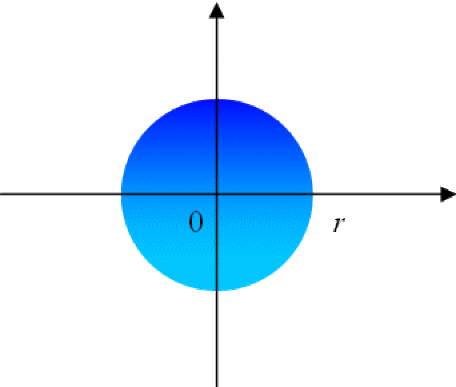
\(D(0,r)\) le disque ouvert défini par : \(D(0,r)=\{z\in C, |z|< r\}\)
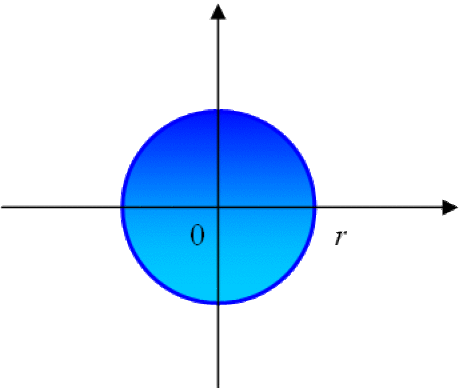
\(\overline{D}(0,r)\) le disque fermé défini par : \(\overline{D}(0,r)=\{z\in C, |z|\leq r \}\)
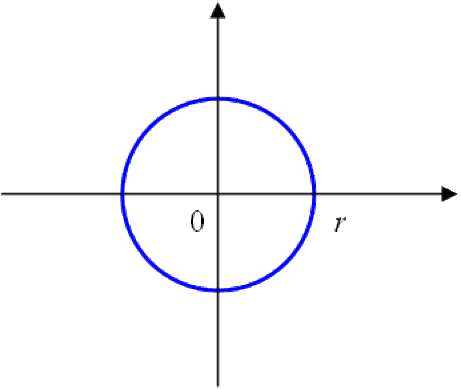
\(C(0,r)\) le cercle défini par : \(C(0,r)=\{z\in C, |z| = r \}\)