Exercice 35
Partie
Question
Étudier la convergence simple et uniforme de la suite de fonctions suivante : n \(\geqslant\) 1, \(f_n(x) = \left \{ \begin{array}{ccc} 2nx& si & x \in \bigg[0 , \frac{1}{2n} \bigg] \\ 2 - 2nx & si& x \in \bigg[\frac{1}{2n} , \frac{1}{n} \bigg] \\ 0 & si & x \geqslant \frac{1}{n} \end{array} \right.\)
Aide simple
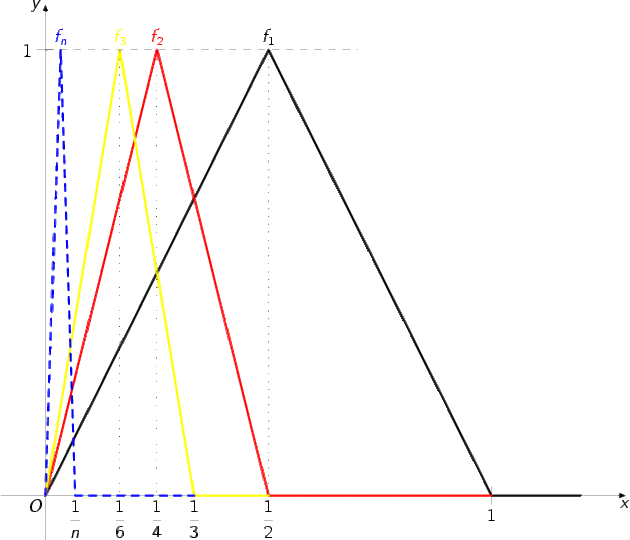
Courbes représentatives de \(f _1\), \(f _2\), \(f _3\) :
Pour x > 0 fixé, on peut toujours trouver\( n_x \in \mathbb{N^*}\) tel que \(x > \frac{1}{n_x}\) par exemple \(n_x = E \left ( \frac{1}{x} \right) + 1\)
Pour n \(\geqslant n_x\),\( f_n(x) = 0\). La suite\(( f_n(x) )_{n \in \mathbb{N}}\) sera nulle à partir d'un certain rang.
La convergence simple ne pose pas de problèmes.
Étudier la convergence uniforme sur\( \mathbb{R_+}\), puis distinguer les sous-ensembles contenant 0 ou pas.
Solution détaillée
Convergence simple
Montrons que la suite de fonctions converge vers la fonction nulle :
Pour x = 0 : \(f_n(0) = 0\) donc \(\displaystyle \lim_{n \rightarrow +\infty } f_n(0) = 0\).
Pour x > 0 : \(\forall \varepsilon > 0, \exists N_{(\varepsilon, X)}, (n \geqslant N \Rightarrow | f_n(x) - 0 |< \varepsilon )\)
Il suffit de prendre \(N_{(\varepsilon, X)} = E \left( \frac{1}{x} \right) + 1\)
La suite (\(f_n\)) converge simplement vers la fonction nulle sur [ 0 ,\(+\infty\) [.
Convergence uniforme sur \( \mathbb{R_+}\)
D'après les courbes représentatives des\( f_n\), pour tout n, \(\underset{x \in \mathbb{R_+}}{max}\Big \{ |f_n(x )- 0| \Big \} = 1\)
Cette quantité ne tend pas vers 0 quand n tend vers \(+\infty\), donc...
La suite (\(f_n\)) ne converge pas uniformément sur \(\mathbb{R_+}\).
Convergence uniforme sur des sous-ensembles de \(\mathbb{R_+}\).
Pour tout a > 0, posons \(n_a = E \left ( \frac{1}{a} \right) + 1\) Alors \(n_a \in \mathbb{N^*}\) et \(\frac{1}{n_a} < a\).
Sur tout intervalle [0, a] : pour n \(\geqslant n_a, max_{x \in [ 0 , a ]}\Big \{ |f_n(x )- 0| \Big \} = 1\), .La suite (\(f_n\)) ne converge pas uniformément sur [0, a].
Sur tout intervalle I du type [a, b] ou [a, \(+\infty\) [ avec b > a > 0 : pour n \(\geqslant n_a\), \(f_n(x) = 0\) sur I.
Donc, pour n \(\geqslant n_a\), \(\underset{x \in l}{max}\Big \{ |f_n(x )- 0| \Big \} = 0\) c'est-à-dire \(\displaystyle \lim_{n \rightarrow +\infty } \bigg( \underset{x \in l}{max}\Big \{ |f_n(x )- 0| \Big \} \bigg)= 0\)
La suite (\(f_n\)) converge uniformément vers la fonction nulle sur toutintervalle [ a , b ] ou [a , \(+\infty\) [ avec b > a > 0.