Exercice 37
Partie
Question
Étudier la convergence simple et la convergence uniforme de la suite de fonctions suivante :
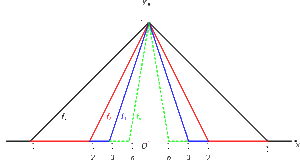
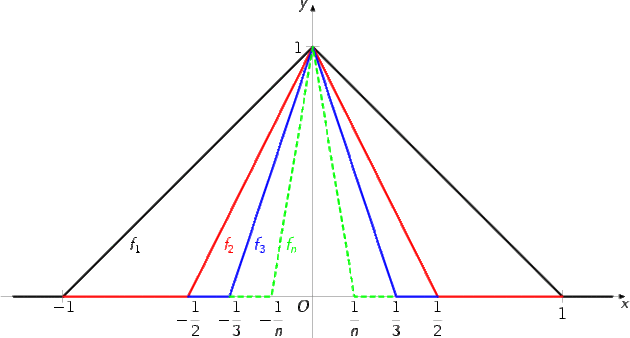
\(n \geq 1,\qquad \left\{ \begin{array}{l l} f_{n}(x) = 0 & \textrm{si}~~|x| > \frac{1}{n} \\ \\ f_{n}(x) = - |nx| + 1 & \textrm{si}~~|x| \leq \frac{1}{n} \end{array} \right.\)
Aide simple
Pour \(x \neq 0\) fixé, on peut toujours trouver \(n_{x} \in \mathbb{N}^{*}\) tel que \(|x| > \frac{1}{n_{x}}\), par exemple \(n_{x} = E \left( \frac{1}{|x|} \right) + 1\).
Pour \(n \geq n_{x}, f_{n}(x) = 0\).
La suite \(\left(f_{n}(x)\right)_{n \geq 1}\) sera égale à 0 à partir d'un certain rang.
Étudier la convergence uniforme sur \(\mathbb{R}^{+}\), puis distinguer les sous-ensembles contenant 0 ou pas.
Solution détaillée
Convergence simple
Si \(x \neq 0\), pour \(n \geq E \left( \frac{1}{|x|} \right) + 1\), \(f_{n}(x) = 0\) donc : \(\forall x \in \mathbb{R}^{*}, \underset{n \rightarrow +\infty}{\textrm{lim}} f_{n}(x) = 0\) ;
Pour \(x = 0\), \(f_{n}(0) = 1\), donc \(\underset{n \rightarrow +\infty}{\textrm{lim}} f_{n}(0) = 1\).
La suite (\(f_{n}\)) converge simplement vers la fonction \(f\) ainsi définie : \(\left\{ \begin{array}{l l} f(x) = 0, & x \neq 0 \\ f(0) = 1 & \end{array} \right.\)
Convergence uniforme sur \(\mathbb{R}\)
Si la suite (\(f_{n}\)) convergeait uniformément sur \(\mathbb{R}\), ce serait vers \(f\) décrite dans le paragraphe précédent.
Or toutes les fonctions \(f_{n}\) sont continues et la limite simple \(f\) ne l'est pas sur \(\mathbb{R}\) ni sur tout intervalle contenant 0, puisque \(f\) n'est pas continue en 0.
La suite (\(f_{n}\)) ne converge pas uniformément sur \(\mathbb{R}\) ni sur tout intervalle de type \([a, b]\) , avec \(a < 0 < b\).
Convergence uniforme sur certains sous-ensembles de \(\mathbb{R}\)
Soit I un intervalle du type \([a ,b]\) ou \([a, +\infty[\) avec \(b > a >0\).
Posons \(n_{a} = E \left( \frac{1}{a} \right) + 1\), alors \(n_{a} \in \mathbb{N}^{*}\) et \(\frac{1}{n_{a}} < a\).
Pour \(n \geq n_{a}\) et pour \(x \in I\), \(f_{n}(x) = 0\) sur \([a, b]\) ou \([a, +\infty[\).
Donc, pour \(n \geq n_{a}\), \(\underset{x \in I}{\textrm{max}} \left\{ \left| f_{n}(x) - 0\right| \right\} = 0\), c'est-à-dire : \(\underset{n \rightarrow +\infty}{\textrm{lim}} \left( \underset{x \in I}{\textrm{max}} \left\{ \left| f_{n}(x) - 0\right|\right\}\right) = 0\).
La suite (\(f_{n}\))converge uniformément vers la fonction nulle sur tout intervalle \([a, b]\) ou \([a, +\infty[\) avec \(b > a > 0\).
De même, par symétrie
La suite (\(f_{n}\)) converge uniformément vers la fonction nulle sur tout intervalle \([a, b]\) ou \(]-\infty, b]\) avec \(a < b < 0\).