Equivalence triangle-étoile
Partie
Question
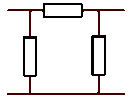
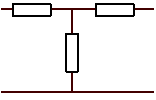
Pour les deux réseaux ci-dessous, exprimer en fonction des éléments la résistance du dipôle équivalent au réseau vu de \(A~ \textrm{et}~B\) quand \(C\) n'est relié à rien; en déduire :
la résistance du dipôle équivalent au réseau vu de\( \displaystyle{B \textrm{ et }C}\)
la résistance du dipôle équivalent au réseau vu de \(\displaystyle{C \textrm{ et }A}\)
les relations que doivent vérifier \(\displaystyle{R_{ab}, R_{bc}, R_{ac}}\) d'une part, et \(\displaystyle{R_A, R_B, R_C}\) d'autre part pour que les deux montages soient équivalents.
Aide simple
Remplacer les dipôles en série par leur résistance équivalente, puis les dipôles en parallèle par leur résistance équivalente.
Aide détaillée
Dans le montage en étoile, une des bornes n'est reliée à rien, le dipôle correspondant ne sera parcouru par aucun courant, et donc n'intervient pas dans le calcul de la résistance équivalente.
Solution simple
1) \(\displaystyle{R_{BC}=R_B+R_C=\frac{R_{bc}.(R_{ab}+R_{ac})}{R_{ab}+R_{bc}+R_{ac}}}\)
2) \(\displaystyle{R_{AC}=R_A+R_C=\frac{R_{ac}.(R_{ab}+R_{bc})}{R_{ab}+R_{bc}+R_{ac}}}\)
3) \(\displaystyle{R_A=\frac{R_{ab}.R_{ac}}{R_{ab}+R_{bc}+R_{ac}}}\)
\(\displaystyle{R_{ab}=\frac{R_A.R_B+R_B.R_C+R_C.R_A}{R_C}}\)
Les autres équivalences s'obtenant par permuation circulaire des indices \(\displaystyle{A, B, C \textrm{ et }a, b, c}\).
Solution détaillée
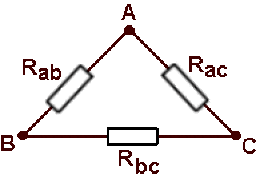
1- Triangle
Le réseau en triangle comporte deux branches en parallèle :
une branche ne comportant qu'un seul dipôle, de résistance \(\displaystyle{R_{ab}}\)
une branche passant par \(C\), formée de deux dipôles en série, de résistances \(\displaystyle{R_{ac} \textrm{ et }R_{bc}}\) ; la résistance équivalente à cette branche est donc ( \(\displaystyle{R_{ab}+R_{bc}}\))
la conductance des deux branches est égale à la somme des conductances
\(\displaystyle{G_{AB}=\frac{1}{R_{AB}}=\frac{1}{R_{ab}}+\frac{1}{R_{ac}+R_{bc}}}\)
Vu de \(\displaystyle{A \textrm{ et }}B\), le triangle a donc pour résistance
\(\displaystyle{R_{AB}=\frac{R_{ab}(R_{ac}+R_{bc})}{R_{ab}+R_{ac}+R_{bc}}}\)
en permutant les indices, on obtient :
\(\displaystyle{R_{AC}=\frac{R_{ac}(R_{ab}+R_{bc})}{R_{ab}+R_{bc}+R_{ac}} ;R_{BC}=\frac{R_{bc}(R_{ab}+R_{ac})}{R_{ab}+R_{bc}+R_{ac}}}\)
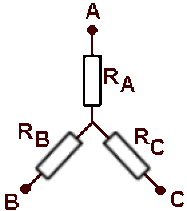
2- Etoile
Si on relie les bornes \(\displaystyle{A \textrm{ et }B}\) à un générateur, un courant circule à travers \(\displaystyle{R_A~ \textrm{et}~ R_B}\). C n'étant relié à rien, aucun courant ne passe dans \(R_C\).
Donc \(\displaystyle{R_{AB}=R_A+R_B}\)
Par permutation des indices
\(\displaystyle{R_{AC}=R_A+R_C ; R_{BC}=R_B+R_C}\)
3- Equivalence triangle-étoile :
Les deux réseaux sont équivalents si, vu des mêmes bornes, ils ont la même résistance équivalente. D'où les trois égalités :
\(R_{AB}=R_{A}+R_{B}= \frac{R_{ab}(R_{ac} + R_{bc})}{R_{ab} + R_{ac} + R_{bc}}\)
\(R_{AC}=R_{A}+R_{C}= \frac{R_{ac}(R_{ab} + R_{bc})}{R_{ab} + R_{bc} + R_{ac}}\)
\(R_{BC}=R_{B}+R_{C}= \frac{R_{bc}(R_{ab} + R_{ac})}{R_{ab} + R_{bc} + R_{ac}}\)
La différence entre les deux premières égalités donne :
\(R_{B} - R_{C} = \frac{R_{bc}(R_{ab} - R_{ac})}{R_{ab} + R_{bc} + R_{ac}}\)
qui, ajouté à la troisième conduit à :
\(R_{B} = \frac{R_{ab}.R_{bc}}{R_{ab} + R_{bc} + R_{ac}}\)
En permutant les indices, il vient :
\(R_{A} = \frac{R_{ab}.R_{ac}}{R_{ab} + R_{bc} + R_{ac}}\), \(R_{C} = \frac{R_{ac}.R_{bc}}{R_{ab} + R_{bc} + R_{ac}}\)
Ces trois relations permettent de remplacer un réseau en triangle par un réseau en étoile qui sera électriquement équivalent.
Réciproquement :
\(R_{ab} = \frac{R_{A}R_{B} + R_{B}R_{C} + R_{C}R_{A}}{R_{C}}\)
\(R_{bc} = \frac{R_{A}R_{B} + R_{B}R_{C} + R_{C}R_{A}}{R_{A}}\)
\(R_{ac} = \frac{R_{A}R_{B} + R_{B}R_{C} + R_{C}R_{A}}{R_{B}}\)
Ces relations ont moins d'intérêt : la transformation étoile-triangle est plus rarement utilisée.