Lignes de champ : forme et orientation [Les propriétés du champ magnétostatique]

Lignes de champ : forme et orientation

Un courant continu, d'intensité \(\mathsf{I}\), circule dans un conducteur rectiligne, filiforme que l'on suppose infiniment long^[1]. Ce fil est confondu avec l'axe \(Oz\) d'un repère orthonormé direct \(\mathfrak R = (O ; xyz)\).

Il s'agit de déterminer le champ magnétostatique \(\stackrel{\hookrightarrow}{B}(M)\) créé en tout point \(\mathsf{M}\) de l'espace par cette distribution de courant \((\mathfrak{D})\).

Dans un premier temps, le problème consiste à définir l'orientation du champ magnétostatique \(\stackrel{\hookrightarrow}{B}(M)\) magnétostatique en tout point \(\mathsf{M}\) de l'espace et d'en déduire la forme des lignes de champ^[2] correspondantes.

Compte tenu de la forme de la distribution \((\mathfrak{D})\), il convient d'expliciter \(\stackrel{\hookrightarrow}{B}(M)\) dans la base cylindrique locale \(\mathfrak{B} = (\vec e_{\rho}, \vec e_{\phi}, \vec e_z)\).

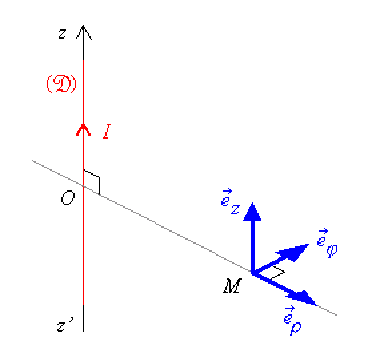
Utilisation des symétries^[3] de la distribution \((\mathfrak{D})\)

L'utilisation des symétries permet, préalablement à tout calcul, de déterminer la direction de \(\stackrel{\hookrightarrow}{B}(M)\) en tout point \(\mathsf{M}\).
\(\stackrel{\hookrightarrow}{B}(M)\) étant un pseudo-vecteur^[4], il est donc perpendiculaire à tout plan de symétrie positive de la distribution qui le crée. Déterminons l'un de ces plans.
- Le plan qui contient \((\mathfrak{D})\) et le point \(\mathsf{M}\) considéré est un plan de symétrie positive car dans une symétrie par rapport à ce plan, \((\mathfrak{D})\) est sa propre image, à la fois géométrique et électrique, le sens du courant étant conservé. \(\stackrel{\hookrightarrow}{B}(M)\) est donc orthogonal en \(\mathsf{M}\) à ce plan.
  On peut écrire \(\stackrel{\hookrightarrow}{B}(M) = B_{\phi}(M) \vec e_{\phi}\) et \(\stackrel{\hookrightarrow}{B}(M)\) est donc orthoradial.
- A ce stade, il convient de garder présent à l'esprit que, lorsqu'on utilise la notation \(\stackrel{\hookrightarrow}{B}(M)\) , cela signifie que le champ magnétostatique, défini en un point \(\mathsf{M}\) quelconque, est fonction des coordonnées de ce point, c'est-à-dire ici, de \(\rho\), \(\phi\) et \(z\).
  On peut donc écrire : \(\vec B(M) = B_{\phi}(\rho, \phi , z) \vec e_{\phi}\)

Utilisation des invariances

Elles permettent de déterminer de quelle(s) variable(s) dépend \(\stackrel{\hookrightarrow}{B}(M)\).
- Une rotation de la distribution \(\mathfrak{D}\) autour de l'axe \(Oz\) laisse le système invariant : le champ magnétique \(\stackrel{\hookrightarrow}{B}(M)\) ne dépend donc pas de la variable \(\phi\).
  Ainsi : \(\stackrel{\hookrightarrow}{B}(M) = B_{\phi}(\rho,z)\vec e_{\phi}\)
- Cette distribution étant infinie, une translation suivant l'axe \(Oz\) laisse le système invariant.
  On a donc : \(\vec B(M) = B_{\phi}(\rho)\vec e_{\phi}\)
- Cette relation donne la forme des lignes de champ : ce sont des cercles d'axe \(Oz\) en tous points desquels \(\stackrel{\hookrightarrow}{B}(M)\) est tangent.
  Les lignes de champ de \(\stackrel{\hookrightarrow}{B}(M)\) sont fermées.

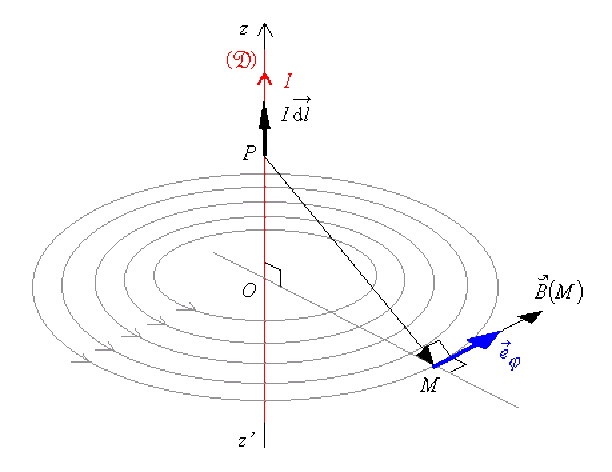
Le sens des lignes de champ est donné par la loi de Biot^[5] et Savart^[6] c'est-à-dire par le produit vectoriel^[7] \(I\overrightarrow{\mathrm{d}l} \wedge \overrightarrow{PM}\) ; ici \(\vec B(M)\) a le sens de \(\vec e_{\phi}\).
On remarque ici que, sur chaque ligne de champ, le module de \(\vec B(M)\) est constant puisqu'il ne dépend que de \(\rho\).

Notes

Infinie (distribution), infiniment long
Deux attitudes sont possibles lorsqu'il s'agit d'étudier les propriétés de l'espace dues à des distributions telles qu'un fil, un cylindre, un disque,... :
- on imagine que la distribution est infinie (une droite, un cylindre infini, un plan,...) et on peut considérer n'importe quel point \(\mathsf{M}\) de l'espace ;
- on sait que la distribution ayant forcément des dimensions finies, le domaine d'étude est restreint à une région limitée, voire très limitée, centrée sur la distribution.
Ligne de champ
Ligne en tout point de laquelle le champ est tangent.
Symétries
Quand les effets d'une distribution sont représentés par un vecteur vrai, ce vecteur est contenu dans les plans de symétrie positive de la distribution et perpendiculaire aux plans de symétrie négative.
Quand les effets d'une distribution sont représentés par un pseudo-vecteur, ce dernier est contenu dans les plans de symétrie négative de la distribution et perpendiculaire aux plans de symétrie positive.
Pseudo-vecteur
On dit aussi vecteur axial. Il est défini par :
- une direction qui est généralement un axe de rotation,
- un sens sur cet axe, lié à la convention adoptée pour l'orientation de l'espace,
- sa norme.
On le distingue des vecteurs polaires par une flèche courbe : \(\stackrel{\hookrightarrow}{B}\)
BIOT (Jean-Baptiste) 1774 - 1862
Mathématicien, astronome et physicien, il collabore avec Gay Lussac pour l'étude du magnétisme terrestre, avec Arago pour la mesure de la densité des gaz et leur indice de réfraction. Avec Savart, il détermine en 1820 le champ magnétique créé par les courants électriques.
SAVART (Félix) 1791 - 1841
Ses études sur l'acoustique le révèlent comme physicien. Il détermine avec Biot en 1820 le champ magnétique créé par les courants électriques. Il est l'inventeur de dispositifs tels qu'une roue dentée qui porte son nom, un polariscope, un sonomètre.
Produit vectoriel
Le produit vectoriel de deux vecteurs \(\overrightarrow V_{\mathit1}\) et \(\overrightarrow V_{\mathit2}\) faisant entre eux un angle \(\theta\in[0,\pi]\) est un vecteur \(\vec P\) noté \(\vec P= \vec{V_1}\wedge\vec{V_2}\), perpendiculaire au plan défini par \(\overrightarrow V_{\mathit1}\) et \(\overrightarrow V_{\mathit2}\), de sens tel que le trièdre \(\overrightarrow V_{\mathit1}\), \(\overrightarrow V_{\mathit2}\), \(\vec P\) soit direct et de norme \(||\vec P||=||\overrightarrow V_{\mathit1}||~.~||\overrightarrow V_{\mathit2}||~.~\sin\theta\).