Circulation du champ magnétostatique créé par un courant filiforme, rectiligne et infiniment long sur un contour fermé [Les propriétés du champ magnétostatique]

Circulation du champ magnétostatique créé par un courant filiforme, rectiligne et infiniment long sur un contour fermé

Considérons la distribution de courant \(\mathfrak{(D)}\) constituée par un conducteur rectiligne, filiforme, supposé infiniment long^[1] et parcouru par un courant continu, d'intensité \(\mathsf{I}\).

Ce fil est confondu avec l'axe \(Oz\) d'un repère orthonormé direct \(\mathfrak{R} = (O ; xyz)\) et \(\mathsf{I}\) circule dans le sens des \(z\) positifs.

Ce que nous savons déjà
- Le champ magnétostatique \(\stackrel{\hookrightarrow}{B}(M)\) créé en tout point \(\mathsf M\) de l'espace par cette distribution de courant \(\mathfrak{(D)}\) est orthoradial et a pour expression \(\vec B(M) = \frac{\mu_0I}{2\pi\rho}\vec e_{\varphi}\).
- Les lignes de champ sont fermées. Ici, ce sont des cercles d'axe \(Oz\) en tous points desquels \(\stackrel{\hookrightarrow}{B}(M)\) est tangent et sur lesquels \(\mathsf B\) garde la même valeur ; ce n'est pas le cas général.

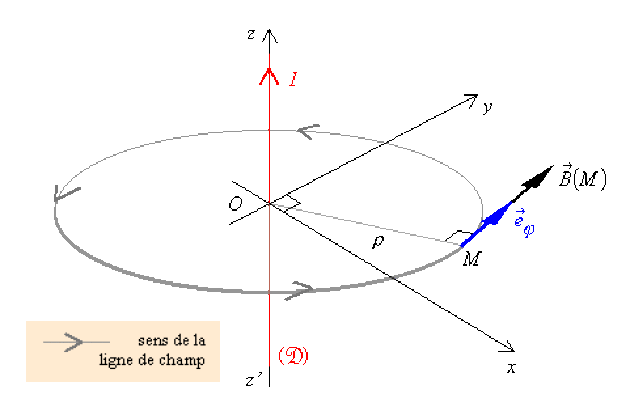
Circulation^[2] de \(\stackrel{\hookrightarrow}{B}(M)\) sur un contour fermé \(\textcircled{C}\) constitué par une ligne de champ.
La circulation de \(\stackrel{\hookrightarrow}{B}(M)\) sur une ligne de champ de rayon \(\rho = OM\) s'écrit :
\(\displaystyle{ \oint_{\textcircled{C}}\stackrel{\hookrightarrow}{B}(M).\overrightarrow{\mathrm{d}l}(M) = \oint_{\textcircled{C}} \frac{\mu_0I}{2\pi\rho}\vec e_{\varphi} . \overrightarrow{\mathrm{d}l} = \oint_{\textcircled{C}} \frac{\mu_0I}{2\pi\rho}\mathrm{d}l_{\varphi} =\oint_{\textcircled{C}} \frac{\mu_0I}{2\pi\rho}\rho \mathrm{d}_{\varphi} = \frac{\mu_0I}{2\pi}\oint_{\textcircled{C}}{\mathrm{d}_{\varphi}}}\)
Noter qu'on distingue deux cas, suivant que la circulation sur \(\textcircled{C}\) qui est un cercle, s'effectue dans le sens direct^[3] ou dans le sens inverse^[4]. En effet, le sens de circulation impose l'orientation du disque délimité par le contour fermé orienté \(\textcircled{C}\) (voir surface ouverte^[5]).

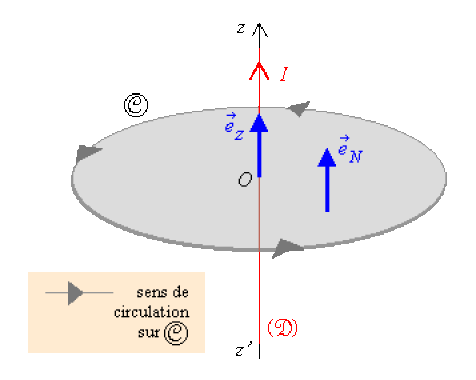
Si la circulation de \(\stackrel{\hookrightarrow}{B}(M)\) s'effectue dans le sens direct :
\(\displaystyle{\frac{\mu_0I}{2\pi} \oint_{\textcircled{C}}\mathrm{d}\varphi = \frac{\mu_0I}{2\pi}\int^{2\pi}_{0}\mathrm{d}\varphi = \mu_0I}\)
On remarque que le courant d'intensité I qui circule dans le conducteur traverse la surface ouverte^[5] du disque délimité par le contour fermé orienté \(\textcircled{C}\) dans le même sens que celui du vecteur unitaire \(\vec e_{N} = \vec e_{z}\) orthogonal au plan du disque.

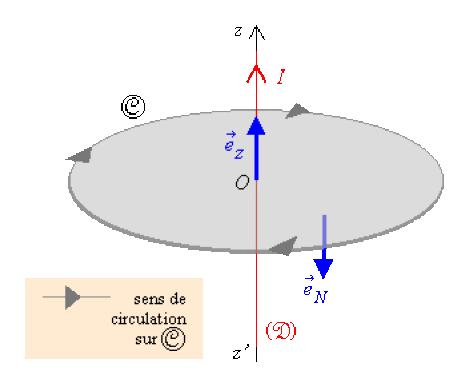
Si la circulation de \(\stackrel{\hookrightarrow}{B}(M)\) s'effectue dans le sens inverse :
\(\displaystyle{\frac{\mu_0I}{2\pi} \oint_{\textcircled{C}}\mathrm{d}\varphi = \frac{\mu_0I}{2\pi} \int^{0}_{2\pi}\mathrm{d}\varphi = -\mu_0I}\)
On remarque alors que le courant d'intensité \(\mathsf{I}\) qui circule dans le conducteur traverse le disque délimité par le contour fermé orienté \(\textcircled{C}\) dans le sens opposé à celui du vecteur unitaire \(\vec e_{N} = -\vec e_z\) orthogonal au plan du disque.

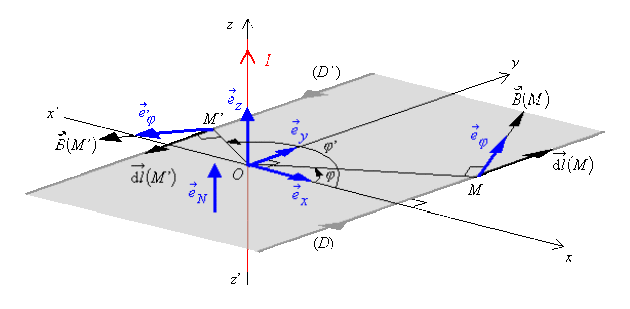
Circulation de \(\stackrel{\hookrightarrow}{B}(M)\) sur un contour fermé \(\textcircled{C}\) constitué par deux droites parallèles \(\mathsf{(D)}\) et \(\mathsf{(D^{'})}\), perpendiculaires au conducteur \(\mathfrak{D}\) et situées du même côté de \(Oz\), dans le plan \(xOy\).
Ces deux droites (infinies) que nous prenons parallèles à \(Oy\), forment un contour fermé si l'on circule sur \(\mathsf{(D)}\) dans le sens des \(\mathsf y\) croissants, en revenant sur \(\mathsf{(D')}\) dans le sens des \(\mathsf y\) décroissants.
Alors, le vecteur unitaire \(\vec e_{N}\) orthogonal à la surface qui s'appuie sur le contour fermé \(\textcircled{C}\) qu'elles forment, est parallèle à \(\vec e_z\) .

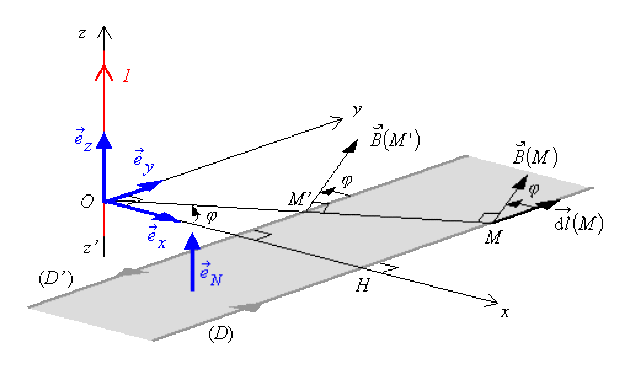
Circulation sur \(\mathsf{(D)}\)
Elle s'écrit : \(\displaystyle{\int_{\mathsf{(D)}}\stackrel{\hookrightarrow}{B}(M) . \overrightarrow{\mathrm{d}l}(M) = \int_{\mathsf{(D)}} \frac{\mu_0I}{2\pi OM}OM \mathrm{d}\varphi}\).
Comme \(OM\mathrm{d}\varphi\) est difficile à expliciter sur \(\mathsf{(D)}\) , on préfère écrire ici :
\(\displaystyle{\int_{\mathsf{(D)}}\stackrel{\hookrightarrow}{B}(M) . \overrightarrow{\mathrm{d}l}(M) = \int_{\mathsf{(D)}}\Big(\frac{\mu_0I}{2\pi OM}\vec e_{\varphi}\Big)\big(\mathrm{d}y \vec e_y\big) = \frac{\mu_0I}{2\pi}\int_{\mathsf{(D)}} \frac{\cos \varphi}{OM}\mathrm{d}y}\) .
Lorsque \(\stackrel{\hookrightarrow}{B}(M)\) circule sur \(\mathsf{(D)}\), \(OM\), \(y\) et \(\varphi\) varient simultanément : ce sont des variables liées et il est pratiquement toujours plus aisé de conserver la variable angulaire.
Ainsi avec \(HM = y = OH \tan\varphi\) , \(\mathrm{d}y = \frac{OH\mathrm{d}\varphi}{\cos^2\varphi}\) et \(OM = \frac{OH}{\cos\varphi}\)
il vient : \(\int_{\mathsf{(D)}} \stackrel{\hookrightarrow}{B}(M) . \overrightarrow{\mathrm{d}l}(M) = \frac{\mu_0I}{2\pi}\int^{+\frac{\pi}{2}}_{-\frac{\pi}{2}}\mathrm{d}\varphi = \frac{\mu_0I}{2}\)
Circulation sur \(\mathsf{(D')}\)
Compte-tenu du sens indiqué, on a :
\(\int_{\mathsf{(D)}} \stackrel{\hookrightarrow}{B}(M') . \overrightarrow{\mathrm{d}l}(M') = \frac{\mu_0I}{2\pi}\int^{-\frac{\pi}{2}}_{+\frac{\pi}{2}}\mathrm{d}\varphi = -\frac{\mu_0I}{2}\)
Notons que, compte tenu du sens de circulation sur \(\mathsf{(D')}\) , on intègre de \(+\pi/2\) à \(-\pi/2\).
Finalement on a :
\(\displaystyle{\oint_{\textcircled{C}}\stackrel{\hookrightarrow}{B} . \overrightarrow{\mathrm{d}l} = \int_{\mathsf{(D)}}\stackrel{\hookrightarrow}{B} . \overrightarrow{\mathrm{d}l} + \int_{\mathsf{(D')}}\stackrel{\hookrightarrow}{B} . \overrightarrow{\mathrm{d}l} = \frac{\mu_0I}{2} - \frac{\mu_0I}{2} = 0}\)
L'ensemble des deux droites \(\mathsf{(D)}\) et \(\mathsf{(D')}\) constitue un contour fermé \(\textcircled{C}\) sur lequel la circulation de \(\stackrel{\hookrightarrow}{B}(M)\) est nulle ; notons que, dans ce cas, aucun courant ne traverse la surface délimitée par le contour fermé \(\textcircled{C}\).

Circulation de \(\stackrel{\hookrightarrow}{B}(M)\) sur un contour fermé \(\textcircled{C}\) constitué par deux droites parallèles \(\mathsf{(D)}\) et \(\mathsf{(D')}\), perpendiculaires au conducteur \(\mathfrak{(D)}\) et situées de part et d'autre de \(Oz\), dans le plan \(xOy\).
Choisissons un sens de parcours sur chacune des droites de telle sorte que le vecteur unitaire \(\vec e_{N}\) orthogonal à la surface qui s'appuie sur le contour fermé qu'elles forment soit parallèle à \(\vec e_{z}\).

Circulation sur \(\mathfrak{(D)}\)
Compte-tenu des calculs précédents, on a :
\(\displaystyle{\int_{\mathfrak{(D)}} \stackrel{\hookrightarrow}{B}(M) . \overrightarrow{\mathrm{d}l}(M) = \frac{\mu_0I}{2}}\)
Circulation sur \(\mathfrak{(D')}\)
Compte-tenu du sens indiqué, les bornes angulaires de l'intégration passent ici de la valeur \(+\pi / 2\) à la valeur \(+3\pi / 2\) ; on a :
\(\int_{\mathfrak{(D')}} \stackrel{\hookrightarrow}{B'}(M'). \overrightarrow{\mathrm dl}(M') = \frac{\mu_0I}{2}\int^{3\pi/2}_{\pi/2}\mathrm{d}\varphi' = \frac{\mu_0I}{2}\)
Finalement, on a :
\(\displaystyle{\oint_{\textcircled{C}}\stackrel{\hookrightarrow}{B} . \overrightarrow{\mathrm{d}l} = \int_{\mathfrak{(D)}} \stackrel{\hookrightarrow}{B} . \overrightarrow{\mathrm{d}l} + \int_{\mathfrak{(D')}}\stackrel{\hookrightarrow}{B} \overrightarrow{\mathrm{d}l} = \frac{\mu_0I}{2} + \frac{\mu_0I}{2} = \mu_0I}\)
La circulation de \(\stackrel{\hookrightarrow}{B}(M)\) le long du contour fermé \(\textcircled{C}\) constitué par les droites \(\mathfrak{(D)}\) et \(\mathfrak{(D')}\) est égale à \(\mu_0I\).
Le courant \(\mathsf{I}\) traversant la surface délimitée par le contour fermé \(\textcircled{C}\) formé par \(\mathfrak{(D)}\) et \(\mathfrak{(D')}\) et son sens coïncidant avec celui du vecteur unitaire \(\vec e_{N}\) orthogonal à la surface délimitée par \(\textcircled{C}\) , la circulation de \(\stackrel{\hookrightarrow}{B}(M)\) sur \(\textcircled{C}\) est positive.

Notes

Infinie (distribution), infiniment long
Deux attitudes sont possibles lorsqu'il s'agit d'étudier les propriétés de l'espace dues à des distributions telles qu'un fil, un cylindre, un disque,... :
- on imagine que la distribution est infinie (une droite, un cylindre infini, un plan,...) et on peut considérer n'importe quel point \(\mathsf{M}\) de l'espace ;
- on sait que la distribution ayant forcément des dimensions finies, le domaine d'étude est restreint à une région limitée, voire très limitée, centrée sur la distribution.
Circulation d'un champ vectoriel
- La circulation du vecteur \(\vec V(M)\) le long de la courbe \((\textcircled{C})\) entre deux points \(A\) et \(B\), est définie par le scalaire :
  \(\displaystyle{\textcircled{C}_{AB}=\int_{\frown{AB}}\overrightarrow V(M)~.~\overrightarrow{\mathrm dl}(M)}\)
  \(M\) étant un point de \((\textcircled{C})\) et \(\overrightarrow{\mathrm dl}(M)\) le vecteur déplacement élémentaire tangent à \((\textcircled{C})\) au point \(M\).
- Soit, dans un repère orthonormé direct \(\mathfrak R = (O~;\vec e_x, \vec e_y, \vec e_z)\), un champ vectoriel \(\overrightarrow V(M)\) et un point \(M\) de coordonnées \(x\), \(y\) et \(z\) appartenant à une courbe orientée \((\textcircled{C})\) quelconque avec :
  \(\overrightarrow V(M)=V_x\vec e_x~+~V_y\vec e_y~+~V_z\vec e_z\)
  et
  \(\overrightarrow{\mathrm dl}(M)={\mathrm dl}_x~\vec e_x~+~{\mathrm dl}_y~\vec e_y~+~{\mathrm dl}_z~\vec e_z=\mathrm dx~\vec e_x~+~\mathrm dy~\vec e_y~+~\mathrm dz~\vec e_z\)
  La circulation de \(\overrightarrow V(M)\) le long de la courbe \((\textcircled{C})\) entre deux points \(A\) et \(B\) s'écrit : \(\displaystyle{\textcircled{C}_{AB}=\int_{\frown AB}~V_x{\mathrm dx}+V_y{\mathrm dy}+V_z{\mathrm dz}}\) .
  La circulation \(\textcircled{C}_{AB}\) est une intégrale curviligne qui dépend, dans le cas général, de la forme de la courbe \(\frown AB\) .'
- Lorsque la circulation du vecteur \(\overrightarrow V(M)\) le long de la courbe \((\textcircled{C})\) entre deux points \(A\) et \(B\) ne dépend pas du chemin suivi pour aller de \(A\) à \(B\), alors :
  On peut écrire \(\displaystyle{\textcircled{C}_{AB}=\int_{\frown{AB}}~\overrightarrow V~.~\overrightarrow{\mathrm dl}=f(B)-f(A)=\int_{\frown{AB}}~\mathrm df}~,\)
  \(f(A)\) et \(f(B)\) étant les valeurs prises par la fonction potentiel \(f(M)\) aux points \(A\) et \(B\).
  La circulation est nulle le long d'un contour fermé quelconque ( \(f(B)=f(A)\) ) : on dit que cette circulation est conservative.
Sens direct ou sens trigonométrique
Sens inverse à celui dans lequel se déplacent les aiguilles d'une montre.
Sens inverse ou sens rétrograde
Sens dans lequel se déplacent les aiguilles d'une montre.
Surface ouverte
Une surface ouverte \(\mathfrak{(S)}\) est une surface pourvue d'une "ouverture" unique délimitée par un contour fermé \(\textcircled{C}\).
On peut se représenter ce type de surface en l'imaginant matérielle et rigide ; un liquide ne pourrait pas y être maintenu car il pourrait s'échapper par l'ouverture.
- On oriente une surface ouverte \(\mathfrak{(S)}\) en définissant en tout point \(\mathsf{M}\) de \(\mathfrak{(S)}\), un vecteur unitaire \(\vec e_{N}\) orthogonal à \(\mathfrak{(S)}\) dont le sens est lié au sens de parcours choisi sur le contour fermé \(\textcircled{C}\).
  Lorsque ce sens de parcours sur \(\textcircled{C}\) est choisi, le sens de \(\vec e_{N}\) est donné par le sens de progression du tire-bouchon de Maxwell tournant dans le sens de parcours choisi sur \(\textcircled{C}\).
- Si on définit autour du point \(\mathsf{M}\) une surface élémentaire \(\mathrm{d}\mathfrak{S}\) , le vecteur surface élémentaire \(\overrightarrow{\mathrm{d}\mathfrak{S}}\) s'écrit \(\overrightarrow{\mathrm{d}\mathfrak{S}}(M) = \mathrm{d}\mathfrak{S}~\vec e_{N}\)