Les propriétés du champ magnétostatique

• Rotationnel

  • On appelle rotationnel au point \(\mathsf{M}\) du champ vectoriel \(\vec B(M)\), le vecteur que l'on note \(\stackrel{\hookrightarrow}{\mathrm{rot}} \vec B(M)\) défini par la formule de Stokes :

    \(\oint_{\textcircled{C}}\stackrel{\hookrightarrow}{B}(M_{\textcircled{C}}) . \overrightarrow{\mathrm{d}l}(M_{\textcircled{C}}) = \iint_{\mathfrak{S}}\stackrel{\hookrightarrow}{\mathrm{rot}}\vec{B}(M_{\mathfrak{S}}) . \stackrel{\hookrightarrow}{{\mathrm{d}\mathfrak{S}}} (M_{\mathfrak{S}})\)

    \(M_{\textcircled{C}}\) étant un point du contour fermé orienté \(\textcircled{C}\) et \(M_{\mathfrak{S}}\) un point de la surface ouverte \(\mathfrak{(S)}\) s'appuyant sur \(\textcircled{C}\).

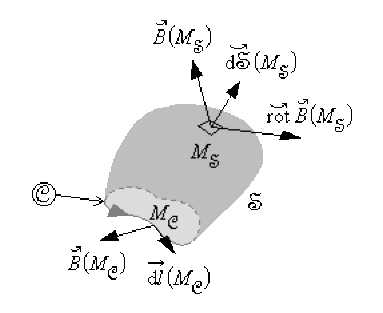
La circulation du champ vectoriel \(\vec B(M)\) le long d'un contour fermé quelconque \(\textcircled{C}\) est égale au flux du champ vectoriel \(\stackrel{\hookrightarrow}{rot}\vec B(M)\) à travers toute surface ouverte \(\mathfrak{(S)}\) s'appuyant sur \(\textcircled{C}\).

• L'opérateur rotationnel fait passer d'un champ vectoriel \(\vec B(M)\) à un autre champ vectoriel \(\stackrel{\hookrightarrow}{rot}\vec B(M)\) ; il peut donner des informations sur le caractère "tourbillonnaire" de \(\vec B(M)\).

• Le théorème d'Ampère qui a pour forme intégrale

  \(\oint_{\textcircled{C}}\stackrel{\hookrightarrow}{B} . \overrightarrow{\mathrm{d}l} = \mu_0 \iint_{\mathfrak{S}} \vec J . \stackrel{\hookrightarrow}{\mathrm{d}\mathfrak{S}}\)

  s'écrit, en précisant les notations,

  \(\oint_{\textcircled{C}}\stackrel{\hookrightarrow}{B}(M_{\textcircled{C}}) . \overrightarrow{\mathrm{d}l}(M_{\textcircled{C}})= \iint_{\mathfrak{S}}\mu_0 \vec J(M_{\mathfrak{S}}) \stackrel{\hookrightarrow}{\mathrm{d}\mathfrak{S}}(M_{\mathfrak{S}})\)

  \(M_{\textcircled{C}}\) étant un point du contour fermé orienté \(\textcircled{C}\) et \(M_{\mathfrak{S}}\) un point de la surface ouverte s'appuyant sur \(\textcircled{C}\).

  La formule de Stokes

  \(\oint_{\textcircled{C}} \stackrel{\hookrightarrow}{B}(M_{\textcircled{C}}).\overrightarrow{\mathrm{d}l}(M_{\textcircled{C}})=\iint_{\mathfrak{S}} \stackrel{\hookrightarrow}{\mathrm{rot}}\vec{B}(M_{\mathfrak{S}}).\stackrel{\hookrightarrow}{\mathrm{d}\mathfrak{S}}(M_{\mathfrak{S}})\)

  permet d'obtenir par identification l'équation locale :

  \(\stackrel{\hookrightarrow}{rot} \vec{B}(M_{\mathfrak{S}}) = \mu_0 \vec J(M_{\mathfrak{S}})\).

  Le rotationnel du champ \(\stackrel{\hookrightarrow}{B}\) au point \(M_{\mathfrak{S}}\) de \((\mathfrak{S})\) est égal au produit par \(\mu_0\) du vecteur densité de courant \(\vec J(M_{\mathfrak{S}})\) défini au même point \(M_{\mathfrak{S}}\) de \((\mathfrak{S})\).