Calcul du champ magnétostatique : théorème d'Ampère
On généralise les résultats relatifs au champ magnétostatique d'un courant filiforme rectiligne, infiniment long.
Théorème : Théorème d'Ampère
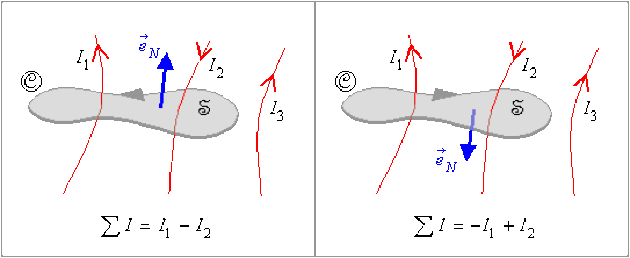
Dans le vide, la circulation du champ magnétostatique \(\stackrel{\hookrightarrow}{B}\) le long d'une courbe de forme quelconque mais fermée \(\textcircled{C}\) est égale au produit par \(\mu_0\) de la somme algébrique des intensités des courants qui traversent une surface \(\mathfrak{(S)}\) s'appuyant sur le contour orienté \(\textcircled{C}\).
\(\oint_{\textcircled{C}}\stackrel{\hookrightarrow}{B} . \overrightarrow{\mathrm{d}l} =\mu_0 \sum I = \mu_0\iint_{\mathfrak{S}}\vec J .\stackrel{\hookrightarrow}{\mathrm{d}\mathfrak{S}}\)
Si le sens du courant est le même que celui du vecteur unitaire \(\vec e_N\) orthogonal à la surface \(\mathfrak{(S)}\) qui s'appuie sur le contour fermé \(\textcircled{C}\), \(\mathsf{I}\) est compté positivement ; si le sens du courant est l'inverse de celui du vecteur unitaire \(\vec e_N\), \(\mathsf{I}\) est compté négativement.
Remarque :
le sens du vecteur unitaire \(\vec e_N\) étant déterminé par le sens de circulation choisi sur \(\textcircled{C}\), \(\mathsf{I}\) est un pseudo-scalaire[2] qu'il faudrait noter \(\mathsf{I^*}\) pour être cohérent avec la notation des pseudo-vecteurs \(\stackrel{\hookrightarrow}{B}\) et \(\stackrel{\hookrightarrow}{\mathrm{d}\mathfrak{S}}\). Toutefois, nous n'alourdirons pas les notations et n'indiquerons pas le caractère pseudo-scalaire de \(\mathsf{I}\).