Travail des forces magnétiques dans le cas d'un déplacement élémentaire [Forces et travail en magnétostatique]

Travail des forces magnétiques dans le cas d'un déplacement élémentaire

Considérons un circuit filiforme \(\mathfrak{D}\) rigide, parcouru par un courant d'intensité \(\mathsf{I}\) et placé dans un champ magnétique \(\stackrel{\hookrightarrow}{B_{\mathrm{ext}}}\). Il est donc soumis à la force de Laplace qui peut provoquer son déplacement et il s'agit de calculer le travail de cette force si un déplacement élémentaire \(\overrightarrow{\mathrm{d} l}_d\) de \(\mathfrak{D}\) se produit.
- L'élément de courant \(I \overrightarrow{\mathrm{d} l}(P)\) est soumis à la force :
  \(\overrightarrow{\mathrm{d}F}_m(P) = I\overrightarrow{\mathrm{d}l}(P) \wedge \stackrel{\hookrightarrow}{B_{\mathrm{ext}}}(P)\)
- Le travail \(\delta w\) de \(\overrightarrow{\mathrm{d}F}_m\) au cours du déplacement \(\overrightarrow{\mathrm{d}l}_d\) a pour expression :
  \(\delta w = \overrightarrow{\mathrm{d}F}_m(P) . \overrightarrow{\mathrm{d}l}_d = [I \overrightarrow{\mathrm{d}l}(P) \wedge \stackrel{\hookrightarrow}{B_{\mathrm{ext}}}(P)] . \overrightarrow{\mathrm{d}l}_d\)
  Le produit mixte^[1] peut s'écrire d'une autre manière, ce qui donne :
  \(\delta w = I[\overrightarrow{\mathrm{d}l}_d \wedge \overrightarrow{\mathrm{d}l}(P)] . \stackrel{\hookrightarrow}{B_{\mathrm{ext}}}(P)\)

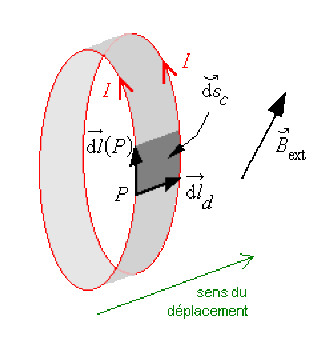
En posant \(\stackrel{\hookrightarrow}{\mathrm{d}s}_c = \overrightarrow{\mathrm{d}l}_d \wedge \overrightarrow{\mathrm{d}l} (P)\) on peut écrire :
\(\delta w = I \stackrel{\hookrightarrow}{\mathrm{d}s}_c . \stackrel{\hookrightarrow}{B_{\mathrm{ext}}}(P)\)
\(\mathrm{d}s_c\) est l'aire de la surface balayée ou "coupée" par \(\overrightarrow{\mathrm{d}l}(P)\) au cours du déplacement \(\overrightarrow{\mathrm{d}l}_d\) ; son orientation est déterminée par le produit vectoriel^[2] : \([\overrightarrow{\mathrm{d}l}_d \wedge \overrightarrow{\mathrm{d}l}(P)]\)
En appelant \(\delta\phi_c\) le flux coupé par \(\overrightarrow{\mathrm{d}l}(P)\), on a : \(\delta w = I \delta\phi_c\)

Le travail effectué au cours du déplacement \(\overrightarrow{\mathrm{d}l}_d\) par l'ensemble de toutes les forces de Laplace agissant sur tous les éléments du circuit est : \(\delta W = I \delta\Phi_c\)
Ce résultat est vrai même en régime variable car il découle directement de la relation de Lorentz.

Notes

Produit mixte
Étant donné trois vecteurs \(\vec V_1\), \(\vec V_2\) et \(\vec V_3\), leur produit mixte est un scalaire \(\mathsf{p}\) tel que \(p = (\vec V_1 \wedge \vec V_2).\vec V_3\). Ce produit est invariant si on effectue une permutation circulaire sur les trois vecteurs. Ainsi : \(p = (\vec V_1 \wedge \vec V_2).\vec V_3 = (\vec V_3 \wedge \vec V_1).\vec V_2 = (\vec V_2 \wedge \vec V_3) . \vec V_1\)
\(\mathsf{P}\) représente le volume du parallélépipède construit sur \(\vec V_1\), \(\vec V_2\) et \(\vec V_3\). En effet, en posant\( \vec P = (\vec V_1 \wedge \vec V_2)\), on a :
\(p = (\vec V_1 \wedge \vec V_2).\vec V_3 = \vec P .\vec V_3 = \parallel \vec P\parallel \parallel\vec V_3\parallel \cos \alpha = \parallel\vec P \parallel . h\)
Appliquée au champ magnétique la permutation donne :
\((\vec v \wedge \vec B) . \vec v = ( \vec v \wedge \vec v).\vec B = \vec0\) car \(\parallel \vec v \wedge \vec v\parallel = v^2 \sin(\vec v,\vec v) = v^2\sin(0) = 0\)
Produit vectoriel
Le produit vectoriel de deux vecteurs \(\overrightarrow V_{\mathit1}\) et \(\overrightarrow V_{\mathit2}\) faisant entre eux un angle \(\theta\in[0,\pi]\) est un vecteur \(\vec P\) noté \(\vec P= \vec{V_1}\wedge\vec{V_2}\), perpendiculaire au plan défini par \(\overrightarrow V_{\mathit1}\) et \(\overrightarrow V_{\mathit2}\), de sens tel que le trièdre \(\overrightarrow V_{\mathit1}\), \(\overrightarrow V_{\mathit2}\), \(\vec P\) soit direct et de norme \(||\vec P||=||\overrightarrow V_{\mathit1}||~.~||\overrightarrow V_{\mathit2}||~.~\sin\theta\).