Courbe engendrée par variation d'une coordonnée (en sphérique)
Durée : 6 mn
Note maximale : 6
Question
On détermine la position \(M\) d'un événement dans l'espace, par rapport à un repère direct formé de trois axes rectangulaires \((O : x, y, z)\), au moyen du système de coordonnées sphériques : \(M\rightarrow M(r,\theta,\varphi)\).
A l'aide de schémas, montrez quelle courbe décrit le point \(M\) lorsqu'on fait varier une coordonnée, les deux autres restant constantes.
Solution
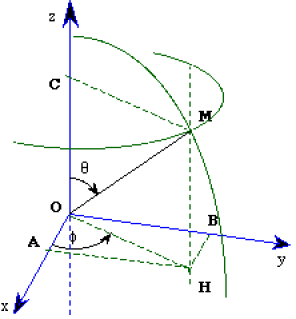
Lorsqu'on fixe \(\theta\) et \(\varphi\), la direction \(OM\) est fixée et \(M\) se déplace sur la demi-droite \([OM)\) quand \(r\) varie.
(2 points)
Lorsque \(r\) et \(\theta\) sont fixés, \(M\) se déplace dans un plan horizontal, sur le cercle de rayon \(CM = r \sin\theta\) centré en \(C\) quand \(\varphi\) varie.
(2 points)
Lorsque \(r\) et \(\varphi\) sont fixés, \(M\) se déplace dans un plan \(COH\) sur un demi-cercle de rayon \(OM =r\) centré en \(O\) quand \(\theta\) varie.
(2 points)
Rappel :
\(\overline{OM}=r\ge0\)
\((\vec{Ox},\vec{OM})=\theta\) avec \(0\le\theta\le\pi\)
\((\vec{Ox},\vec{OH})=\varphi\) , \(0\le\varphi\le2\pi\)
\(C=M (r\cos\theta,0,\varphi)\)
\(\displaystyle{H =M (r\sin\theta,\frac\pi2,\varphi)}\)