Uniformité du champ de vecteurs u (en sphérique)
Durée : 5 mn
Note maximale : 5
Question
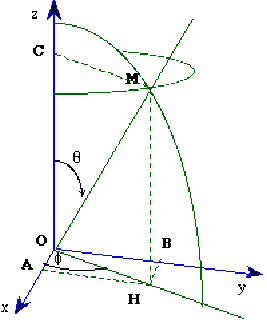
On détermine la position \(M\) d'un événement dans l'espace, par rapport à un repère direct formé de trois axes rectangulaires \((O, x, y, z)\), au moyen du système de coordonnées cylindriques : \(M\rightarrow M(r,\theta,\varphi)\).
A l'aide de schémas, rappelez quelles courbes décrit le point \(M\) lorsqu'on fait varier une coordonnée, les deux autres restant constantes.
On appelle \(d\vec{(u_j)}_i\) l'accroissement infinitésimal de \(\vec{u_j}\) produit par l'accroissement de \(i\) seul.
Déterminez les couples \(i\), \(j\) tels que \(\displaystyle{ \frac {\vec{du_j}} {di} }\) où \(i\) et \(j\) sont \(r\), \(\theta\) ou \(\varphi\).
Solution
Lorsque \(r\) varie, \(M\) se déplace sur la demi-droite \(OM\). Les vecteurs subissent une translation et restent donc invariants.
On a donc \(\displaystyle{ \frac {\vec{du_j}} {dr} = \vec{0}}\).
(2 points)
Lorsque \(\theta\) varie, \(M\) se déplace sur le demi-cercle de rayon \(OM = r\) dans le plan \(zOM\).
Seul \(\vec{u_\varphi}\) , perpendiculaire à ce plan, reste invariant :
\(\displaystyle{ \frac {\vec{du_\varphi}} {d\theta} = \vec{0}}\).
(2 points)
Lorsque \(\varphi\) varie, \(M\) se déplace, dans le plan \(xCy\), sur un cercle de rayon \(CM\).
Tous les vecteurs unitaires ont leurs directions qui varient.
(1 point)