Pendule (2)
Durée : 10 mn
Note maximale : 10
Question
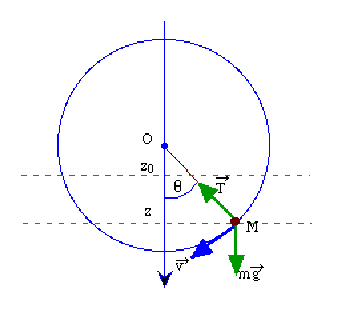
Un objet de petite taille de masse m qu'on peut assimiler à un point matériel est relié par un fil inextensible de longueur a et de masse négligeable à un point fixe \(O\).
Il est abandonné sans vitesse initiale à une altitude inférieure à celle de \(O\).
Montrez comment la conservation de l'énergie du point matériel sur un cercle situé dans un plan vertical peut être exprimée en fonction de la composante du moment cinétique par rapport à l'axe perpendiculaire à ce plan et passant par \(O\).
Montrez comment cette relation permet de trouver l'expression de la vitesse angulaire en fonction de l'angle \(\theta\) qui repère la position du point matériel sur le cercle à partir de la verticale orientée vers le sol.
Établissez l'expression de la vitesse angulaire dans le cas de petits mouvements autour de la position d'équilibre et trouvez comment \(\theta\) varie avec le temps.
Solution
Le point matériel est soumis à l'action de la pesanteur: \(\vec{F}=mg\vec{u_z}\) avec \(g>0\)
Il est également soumis à la tension du fil mais, celui-ci étant toujours perpendiculaire au déplacement, la tension ne travaille pas.
(2 points)
Ainsi, l'énergie mécanique \(E\) du pendule dans le champ de pesanteur est conservée :
\(\displaystyle{E=\frac{{L_y}^2}{2ma^2}-mgz+U_0}\).
Si on repère la position du point matériel sur le cercle par l'angle \(\theta\) tel que
\(z=a\cos\theta\ge0\),
(2 points)
cela s'écrit aussi :
\(\displaystyle{\frac{{L_y}^2}{2ma^2}=mga(\cos\theta-\cos\theta_0)}\).
(1 point)
(1 point)
Comme \(\displaystyle{L_y=ma^2\frac{d\theta}{dt}}\), il vient
\(\displaystyle{\left(\frac{d\theta}{dt}\right)^2=2\frac{g}{a}(\cos\theta-\cos\theta_0)}\),
(1 point)
et pour de petits angles
\(\displaystyle{\frac{d\theta}{dt}=\sqrt{\frac{g}{a}({\theta_0}^2-\theta^2)}}\).
(2 points)
Après séparation des variables, on obtient
\(\displaystyle{\frac{d\theta}{\sqrt{{\theta_0}^2-\theta^2}}=\sqrt{\frac{g}{a}}dt}\)
dont la solution est
\(\theta=\theta_0\cos\omega_at\) avec \(\displaystyle{\omega_a=\sqrt{\frac{g}{a}}}\).