Marcheur sur un plateau tournant
Durée : 10 mn
Note maximale : 10
Question
La vitesse d'un homme, par rapport au référentiel lié au solide sur lequel il se déplace en marchant, est invariante et égale à \(v_0\).
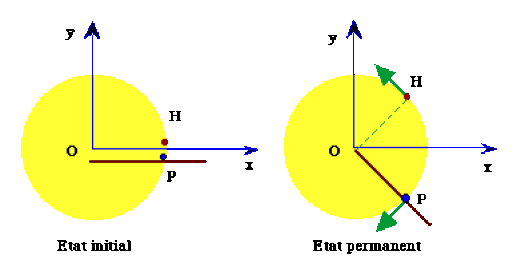
Initialement, cet homme \(H\) est au repos à la distance \(d\) de l'axe d'un plateau circulaire \(P\) immobile par rapport au sol \(S\). Puis il se met en mouvement en restant à la distance \(d\) de l'axe : au bout d'un certain temps, sa vitesse par rapport à \(P\) atteint la valeur \(v_0\).
En supposant qu'il n'y a pas de frottement entre \(P\) et \(S\), calculez la vitesse angulaire \(\omega\) de \(P\) autour de son axe par rapport à \(S\) en fonction de \(m\), masse de \(H\), et de \(I\), moment d'inertie de \(P\) par rapport à son axe.
Vérifiez vos résultats dans des cas extrêmes.
Solution
Puisqu'il faut calculer la vitesse de l'homme par rapport au sol, on adopte le point de vue d'un observateur lié au sol considéré comme un référentiel galiléen.
(1 point)
Le système mécanique formé par l'homme et le plateau est soumis à des forces extérieures dont la résultante est nulle : poids de \(H\) et \(P\) et réaction de \(S\), pas de frottement entre \(P\) et \(S\) (mais l'existence de frottement entre \(H\) et \(P\) est essentielle).
(1 point)
Le système étant plongé dans un environnement invariant par rotation autour de l'axe du plateau \(Oz\), la composante \(L_z\) du moment cinétique est conservée.
On a, algébriquement :
\({md^2}_{w/S}+I\Omega_{/S}=0\)
où \(\omega_{/S}\) et \(\Omega_{/S}\) désignent les vitesses angulaires de l'homme \(H\) et du plateau \(P\) par rapport au sol.
(3 points)
On peut introduire la vitesse angulaire \(\omega_0=\omega_{/P}\) de l'homme par rapport au plateau en appliquant la loi de transformation des vitesses angulaires aux référentiels \(S\) et \(P\) :
\(\omega_{/S}=\omega_{/P}+\Omega_{\S}\)
(2 points)
En substituant en fonction de \(\displaystyle{\omega_0=\omega_{/P}=\frac{V_0}{d}}\) , on trouve:
\(\displaystyle{\Omega_{/S}=-\omega_0\frac{md^2}{(I+md^2)}=-v_0\frac{md}{(I+md^2)}}\)
(1 point)
Du fait que \(\Omega_{/S}\) est opposé à \(\omega_0\), on en conclut que le plateau se met en mouvement dans le sens opposé à celui du déplacement de l'homme.
On remarque que le plateau reste pratiquement immobile par rapport à \(S\) lorsque \(I\gg md^2\). A l'inverse, si \(md^2\gg I\), \(\Omega_{/s}=-\omega_0\) et \(\omega_{/S}=0\): cette fois c'est l'homme qui reste immobile par rapport au sol alors que le plateau tourne dans le sens opposé à celui du déplacement de l'homme par rapport au plateau.
(1 point)
(1 point)