Déviation vers l'est
Partie
Question
Déviation vers l'est (*)
Un objet de masse m initialement au repos est laché d'une altitude faible devant le rayon de la terre. En supposant que la vitesse de rotation de la terre sur elle-même est constante, montrer que dans sa chute, l'objet est dévié vers l'Est par rapport à la verticale de son point de départ. On exprimera cette déviation en fonction de la latitude \(\lambda\) du lieu.
Aide simple
En priorité, faire un schéma qui permette de visualiser les données en sphérique. Décomposer les divers vecteurs dans la base cartésienne attachée au point \(O\) de la surface terrestre Supposer que le vecteur vitesse, bien qu'il y ait déviation, garde la même direction qu'à l'instant du lâcher.
Solution détaillée
Etudions le problème dans le référentiel galiléen (\(G,x,y,z\)).
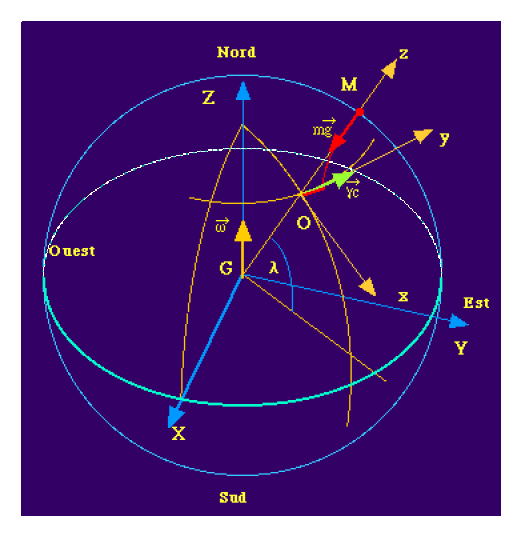
L'objet est laché d'un point \(M\) situé à une altitude \(z\). Il est soumis à l'interaction de gravitation terre-objet qui s'écrit :
\(\displaystyle{\overrightarrow F_G=-G\frac{m_tm}{(R+z)^2}\overrightarrow k\approx-G\frac{m_tm}{R^2}\overrightarrow k}\)
Le principe fondamental de la dynamique donne :
\(\displaystyle{m\overrightarrow\gamma=F\overrightarrow G}\)
en appelant \(\overrightarrow\gamma\) l'accélération de \(M\) par rapport à ( \(G,x,y,z\) ), qui comprend donc les accélérations d'entrainement et de Coriolis.
Mais le poids\( m\overrightarrow g\) de \(M\) est défini comme la différence de la force de gravitation et du produit (masse \(x\) accélération d'entrainement) :
\(\displaystyle{m\overrightarrow g=F\overrightarrow G-m\overrightarrow\gamma_e}\)
D'autre part, en appelant \(\overrightarrow\omega\) le vecteur vitesse instantané de rotation diurne de la terre et le vecteur vitesse instantané de \(M\) dans le référentiel local, l'accélération de Coriolis s'écrit :
\(\displaystyle{\overrightarrow\gamma_c=2\overrightarrow\omega\wedge\overrightarrow v}\)
On suppose en première approximation que le vecteur vitesse a une direction qui diffère peu de la verticale et que l'on \(\overrightarrow a_v=v\overrightarrow k\). Sur la base
\((\overrightarrow i,\overrightarrow j,\overrightarrow k) :\overrightarrow\omega=-\omega\cos\lambda\overrightarrow i+\omega\sin\lambda\overrightarrow k\)
et\( \displaystyle{\overrightarrow\gamma_c=2\;\omega\;v\sin\lambda\overrightarrow j}\)
En reportant dans l'expression du principe fondamental de la dynamique, compte tenu des conditions initiales :
\(\displaystyle{x=0,y=0,z=z_0,x'=0,y'=0,z'=0 :x"=0\Longrightarrow x'=0\Longrightarrow x=0}\)
\(y''=-2\;\omega\;v\;\sin\lambda\)
\(\displaystyle{z"=-g\Longrightarrow z'=-gt\Longrightarrow z=-\frac{1}{2}gt^2+z_0}\)
Pour intégrer y'' il faut expliciter\( \overrightarrow v\) ; mais \(\displaystyle{\overrightarrow v=v\overrightarrow k}\) par suite , d'où :
\(\displaystyle{y"=-2\;\omega\;\sin\;\lambda(-gt)=+2\;\omega\;g\sin\;\lambda t}\)
\(\begin{array}{rcl}y'&=&g\omega\sin\lambda t^2\\y&=&g\omega\sin\lambda\frac{t^3}{3}\end{array}\)
Sur Oz on a un mouvement de chute libre uniformément accéléré; en même temps, on a la déviation y vers l'est due à la force de Coriolis.
On voit que la trajectoire de la particule étant déviée de la verticale, sa vitesse \(\overrightarrow v\) admet une composante non nulle sur\( \overrightarrow j\) . Mais cette composante est très faible, ce qui justifie l'approximation faite plus haut.