Propriétés du champ de gravitation
Champ de forces centrales
Soit le cas d'une répartition sphérique (\(r > R\)), ce qui revient à dire que les sources du champ se ramènent à une source unique ponctuelle placée en \(O\).
Il en résulte que le vecteur champ en tout point de l'espace a sa direction qui passe toujours par le point \(O\). Si nous plaçons en \(M\) une masse test \(m'\), celle-ci est soumise de la part du champ à une force, dont le support passe également toujours par \(O\).
Un tel champ s'appelle un champ de force central.
Si on s'intéresse, non plus au champ de forces mais au champ d'accélération, on dit souvent par abus de langage, que le champ de gravitation est un champ d'accélération centrale.
Potentiel du champ de gravitation
On étudie au sous-chapitre 03 les champs de vecteurs dérivant d'un potentiel scalaire.
Les définitions et principales propriétés y sont étudiées.
Le rotationnel du champ de gravitation est nul.
Il en résulte que le champ de gravitation dérive d'un potentiel scalaire appelé potentiel newtonien, noté \(V\) et que l'on peut écrire:
\(\displaystyle{\overrightarrow A(M)=-\overrightarrow{grad}\;V(M)}\)
La circulation élémentaire du champ est :
\(\displaystyle{\overrightarrow A.d\overrightarrow{M}=-\overrightarrow{grad}\;V(M).d\overrightarrow M=-dV}\)
Pour un déplacement fini, la circulation ne dépend que des valeurs de la fonction potentiel au point de départ (1) et au point d'arrivée (2):
\(\displaystyle{\int_{M_1}^{M_2}\overrightarrow A.\overrightarrow{dr}=V_1-V_2}\)
Remarque:
On écrit indifféremment \(\displaystyle{\overrightarrow{dM}\textrm{ ou }\overrightarrow{dr}\textrm{ ou }\overrightarrow{dl}}\) pour le déplacement vectoriel élémentaire de \(M\).
La circulation du champ de gravitation le long d'un contour fermé \(\displaystyle{\oint_C}\) est nulle:
\(\displaystyle{\oint_C\overrightarrow A.d\overrightarrow r=\overrightarrow0}\)
La fonction potentiel se calcule facilement à partir de l'expression de la circulation élémentaire:
\(\begin{array}{rcl}\overrightarrow A.\overrightarrow{dr}&=&-G\frac{m}{r^2}\overrightarrow u_r.\overrightarrow{dr}=-G\frac{m}{r^2}\overrightarrow u_r.d(r\overrightarrow u_r)\\&=&-G\frac{m}{r^2}dr=-dV\end{array}\)
\(\displaystyle{V(M)-V(M_0)=Gm\int_{r_0}^r\frac{-1}{r^2}dr=-Gm[\frac{1}{r}-\frac{1}{r_0}]}\)
Le potentiel est défini par une différence avec celui, arbitraire, existant en un point \(M_0\). Dans la quasi totalité des cas, on imposera un potentiel nul à l'infini, ce qui permet d'écrire, par abus de langage, \(\displaystyle{V(M)=-G\frac{m}{r}}\).
Énergie potentielle du champ de forces
Si l'on place en \(M\) où le champ vaut \(\displaystyle{\overrightarrow A(M')}\) et le potentiel \(V(M)\), une masse test \(m'\), celle-ci est soumise à une force \(\displaystyle{\overrightarrow F=m'\overrightarrow A}\) ; elle est donc dans un champ de forces dont l'énergie potentielle \(U\) est liée à la fonction potentiel par la relation :
\(\displaystyle{U(M)-U(M_o)=G\;mm'\int_{r_0}^r\frac{-1}{r^2}dr=-Gmm'[\frac{1}{r}-\frac{1}{r_0}]}\)
\(U(M)\) est l'énergie potentielle de gravitation de la particule \(m'\) placée dans le champ de forces gravitationnelles. Remarque:
Il ne faut pas confondre potentiel du champ de gravitation et énergie potentielle d'une particule placée dans ce champ ; en effet,
le potentiel gravitationnel ne dépend que des sources du champ.
l'énergie potentielle est liée à l'interaction masse-champ.
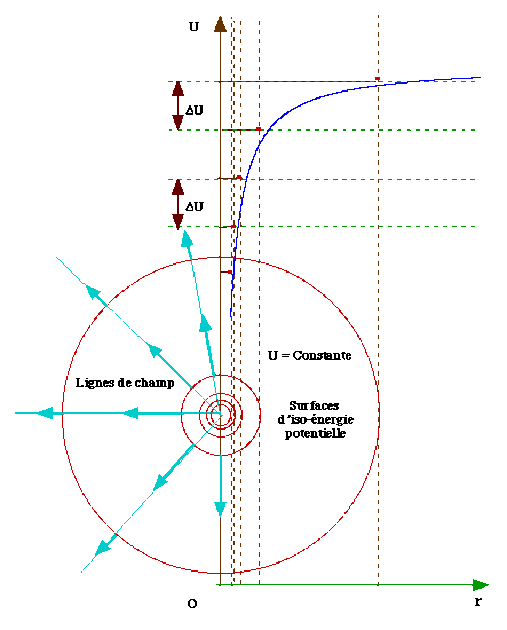
Surfaces équipotentielles
La surface équipotentielle d'une source ponctuelle admet pour équation :
\(\displaystyle{G\frac{m}{r}=\textrm{Constante}}\)
C'est l'équation d'une sphère ayant pour centre la source du champ.
Les surfaces équipotentielles sont des sphères concentriques.
Les lignes de champ sont les trajectoires orthogonales à ces sphères, ce sont des droites passant par le centre du champ : elles sont radiales.
Pour deux sources ponctuelles ou deux répartition de masses sphériques, les surfaces d'égale Energie Potentielle et les lignes du champ de forces sont homothétiques de celles du champ de gravitation.
Mesure de G
C'est à CAVENDISH que l'on doit la mesure directe de la constante de gravitation universelle \(G\) en 1798. L'expérience, très délicate, a été faite avec la balance qui porte son nom; on met en interaction une grosse masse fixe avec une petite masse placée au bout d'un bras horizontal suspendu à un fil de torsion. Les deux masses s'attirent, entraînant une torsion du fil : L'équilibre est réalisé lorsque la torsion compense l'attraction de gravitation.
Si \(C\) est la constante de torsion du fil :
\(\displaystyle{C_{\alpha}=2\;F\;l=2l\;G\frac{mM}{d^2}}\)
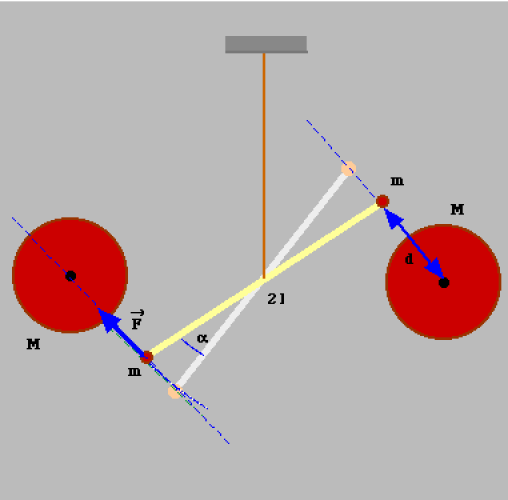
L'ordre de grandeur est le suivant : pour \(m = 50 \textrm{ g}, 2l = 20 \textrm{ cm}, M = 30 \textrm{ kg}\) l'équilibre est réalisé lorsque \(\alpha = 2.10^{-3}\) radians si \(C = 4,5 10^{-7} \textrm{N.m.rd}^{-1}\)
Les forces en jeu, de l'ordre de \(5.10^{-9} N\), sont extrêmement faibles et l'expérience très difficile à réaliser. Elle a cependant permis une première mesure de \(G\).
La valeur actuellement adoptée est :
\(G = (6, 670 \pm 0,005).10^{ -11} \textrm{N. m}^2\textrm{ kg}^{ -2}\)