Champ de gravitation

Considérons un pendule immobile par rapport à la surface de la terre et dont le point matériel \(M\) de masse m est suspendu à un fil tendu; la force de tension du fil est \(\displaystyle{\overrightarrow T}\) ;\( M\) est en un lieu de la surface de la terre à la latitude \(\lambda\); si la terre a pour masse \(M\) la force d'interaction de gravitation de la terre sur \(M\) est \(\displaystyle{\overrightarrow F_G=-G\frac{mM}{R^2}\overrightarrow u_r}\)

Plaçons nous dans le référentiel géocentrique, considéré comme galiléen. et appliquons le principe fondamental de la Dynamique. L'attraction terrestre est \(\displaystyle{\overrightarrow A}\). La force de tension du fil est \(\displaystyle{\overrightarrow T}\) . Le pendule étant immobile par rapport au sol, la vitesse relative et l'accélération relative sont nulles; seule demeure l'accélération d'entraînement : son accélération par rapport à un galiléen est donc égale à l'accélération d'entraînement \(\displaystyle{\overrightarrow{\gamma_e}}\).

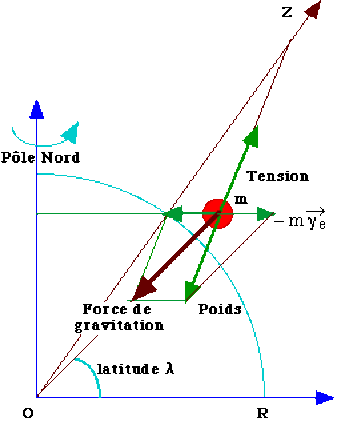
Le Théorème de la quantité de mouvement donne alors :

\(\displaystyle{m\overrightarrow A+\overrightarrow T=m\overrightarrow\gamma=m\overrightarrow\gamma_e}\)

Dans le référentiel terrestre, le poids équilibre la force de tension.

\(\displaystyle{\overrightarrow p=-\overrightarrow T=m(\overrightarrow A-\overrightarrow\gamma_e)}\)

Par définition, on appelle poids la quantité vectorielle opposée à la force de tension.

C'est la composition de l'attraction universelle et de l'opposé de l'accélération d’entraînement.

La direction du fil à plomb indique la verticale du lieu qui ne coïncide pas avec la direction du rayon terrestre.

Si on appelle \(\displaystyle{\overrightarrow g}\) l'accélération de la pesanteur au point \(M\), on retrouve la définition du poids de \(M\):

\(\displaystyle{\overrightarrow p=m\overrightarrow g\textrm{ avec }\overrightarrow g=\overrightarrow A-\overrightarrow\gamma_e}\)

L'ensemble des vecteurs en tout point de la surface de la terre constitue le champ de pesanteur terrestre, il est donné par:

\(\displaystyle{\overrightarrow g=(-G\frac{M}{R^2}+\omega^2R)\cos\lambda\overrightarrow i-G\frac{M}{R^2}\sin\lambda\overrightarrow k}\)

Nous retrouvons que la verticale est donnée par rapport à la direction du fil à plomb. L'horizontale est définie par le niveau de l'eau qui est une équipotentielle du champ de forces de pesanteur terrestre.

Dans ces conditions, "verticale" et "horizontale" sont bien perpendiculaires.

\(\displaystyle{\overrightarrow g}\) dépend de la latitude et, sauf à l'équateur et aux pôles, son support ne passe pas par le centre de la terre supposée sphérique.

La forme réelle de la terre, ou géoïde, est mieux modélisée par un ellipsoïde de révolution que par une sphère.

L'angle \(\displaystyle{\alpha}\) a que fait la verticale d'un lieu \(M\) avec le rayon de la terre \(OM\) est :

\(\displaystyle{\alpha=(\overrightarrow F,\overrightarrow P)\Longrightarrow\textrm{tg}\alpha=\frac{\omega^2R\cos\lambda\sin\lambda}{G\frac{M}{R^2}-\omega^2R\cos^2\lambda}}\)

Pour une latitude de \(45°\), sachant que \(M = 5,98.10^{24}\textrm{ kg}\), l'angle \(\displaystyle{\alpha}\) vaut environ \(6°\). Il sera souvent négligé.

L'accélération de la pesanteur dépend de la latitude du lieu et de l'altitude. On peut déterminer \(g\) par des mesures directes sur la chute libre des corps sous vide. Ces mesures d'accélération sont aujourd'hui très précises et ont remplacé les mesures de périodes d'oscillation de pendules.

On adoptera la valeur moyenne au niveau de la mer : \(g_0 = 9, 8 \textrm{ ms}^{-2}\)

Connaissant \(g_0 \textrm{ et }G\), on en déduit la masse de la terre \(M = 6.10^{24}\textrm{ kg}\)

Connaissant les dimensions géométriques du globe, on en déduit sa densité moyenne; à partir de là, on peut élaborer des modèles de répartition de masses à l'intérieur de la terre.

Nous avons postulé deux lois qui introduisent la notion de masse; la première est le principe fondamental de la dynamique qui postule la proportionnalité de la force appliquée au point matériel à son accélération dans un référentiel galiléen; le coefficient de proportionnalité est appelé masse d'inertie que nous noterons \(m_i\)

\(\displaystyle{\overrightarrow F=m_i\overrightarrow\gamma}\)

La seconde est la loi de Newton qui postule l'existence d'une interaction à distance entre éléments matériels proportionnelle aux masses de chacun de ces éléments; les masses ainsi introduites portent le nom de masse newtonienne ou gravitationnelle que nous noterons \(m_n\)

\(\displaystyle{\overrightarrow{F_G}=-K\frac{m_nm'n}{r^2}\overrightarrow u_r}\)

Les notions de masse d'inertie et de masse de gravitation résultent de deux postulats de la mécanique et rien n'indique, a priori, qu'il s'agit des mêmes quantités.

Pour savoir ce qu'il en est, nous allons reprendre le problème relatif au champ de pesanteur terrestre et à la direction de la verticale.

Considérons un point matériel \(M\) immobile pendu à un fil à plomb à la surface de la terre; il est soumis à la tension du fil et à l'interaction gravitationnelle de la terre. En appelant \(m_n\) et \(m_{nt}\) les masses gravitationnelles du point et de la terre, la force de gravitation s'écrit:

\(\displaystyle{\overrightarrow{F_G}=-K\frac{m_{nt}m_n}{r^2}\overrightarrow u_r}\)

La direction de la verticale en \(M\)(direction du fil à plomb) est donnée par \(\displaystyle{\overrightarrow{F_G}-m\overrightarrow{\gamma_e}}\)

L'angle \(\displaystyle{\alpha}\) a que fait cette verticale avec le rayon de la terre passant par \(M\) est, en différenciant les masses :

\(\displaystyle{\textrm{tg}\;\alpha=\frac{\frac{m_i}{m_n}\omega^2R\sin\lambda\cos\lambda}{G\frac{m_t}{R^2}-\frac{m_i}{m_n}\omega^2R\cos^2\lambda}}\)

Il en résulte que si le rapport des masses d'inertie et de gravitation de \(M\) n'est pas constant, c'est à dire si la masse d'inertie n'est pas proportionnelle à la masse de gravitation, en faisant l'expérience du fil à plomb avec différents objets, on trouvera des directions de la verticale différentes.

De nombreuses expériences ont été faites: quels que soient les corps suspendus au fil à plomb, elles ont toujours données la même direction de la verticale.

Les expériences de Galilée sur la chute des corps suggéraient déjà que l'accélération due au champ de gravitation de la Terre est indépendante de la masse et de la nature des corps. Les premières expériences modernes démontrant cette égalité avec une haute précision sont celles du baron Roland von Eötvös. La précision de ce type d'expérience a été considérablement affinée par R.H. Dicke et V. B. Braginskii (qui utilisaient l'accélération due au champ de gravitation du Soleil) et, plus récemment, par E. G. Adelberger. On sait maintenant, grâce à ces expériences extrêmement délicates, que le rapport entre la masse inertielle et la masse gravitationnelle (qui est constante pour chaque substance) est une constante universelle pour toute la matière, la précision de mesure atteinte étant l'une des meilleures de toute la physique: \(\Delta\alpha/\alpha =10^{-12}\)

Il résulte de ces expériences que les masses d'inertie et gravitationnelles sont proportionnelles, c'est à dire que l'on peut écrire: \(m_i = K m_n\)

La valeur de \(K\) est fixée par le choix du système d'unités; dans le système international utilisé, on a fait le choix le plus simple: \(K =1\), mais rien n'interdit d'en faire un autre.

La valeur de la constante de gravitation résulte de ce choix.