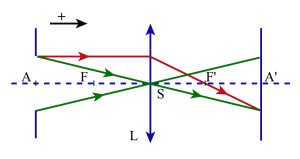
Méthode des points conjugués
applicable aux lentilles convergentes et divergentes
Lentille convergente ( f ' > 0 )
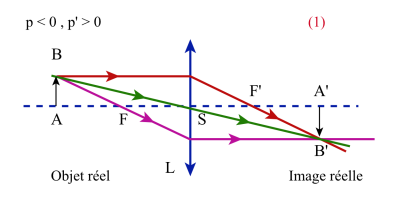
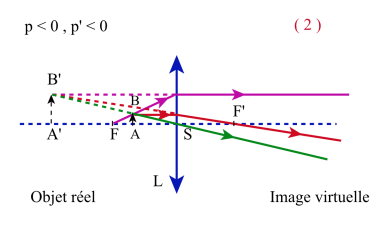
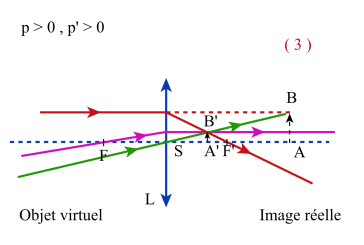
Lentille divergente ( f ' < 0 )
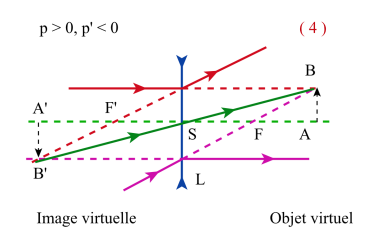
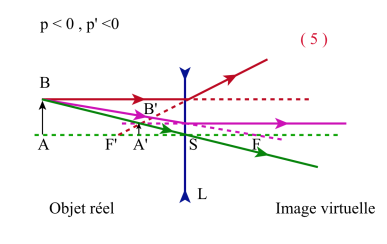
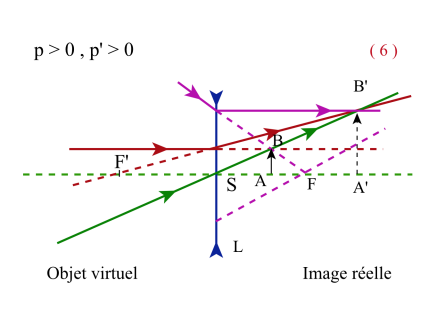
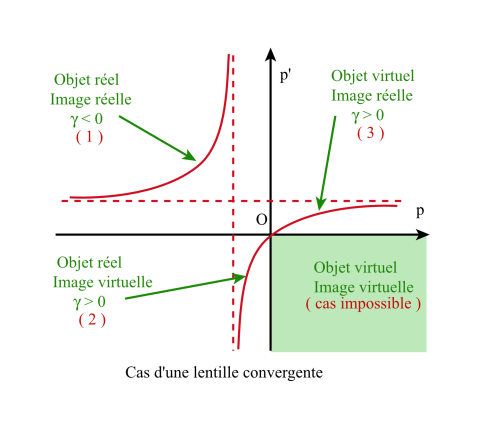
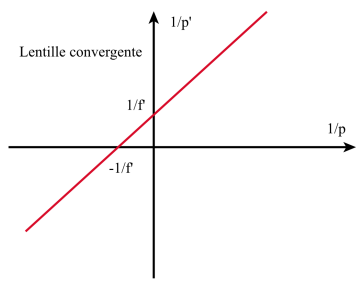
La courbe p' = f ( p ) est une hyperbole équilatère dont les asymptotes sont : p'= f ' et p = - f ' .
Sur la figure ci-contre, pour chacun des quadrants, est précisé, en référence aux figures précédentes, la nature (réelle ou virtuelle) des objets et des images.
Posons \(~y=\frac1{p'}~\) et \(~x=\frac1p\)
La courbe : \(~y=-x+\frac1{f'}~\) est une droite coupant l'axe : 1/p' en 1/f ' et l'axe : 1/p en - 1/f '.
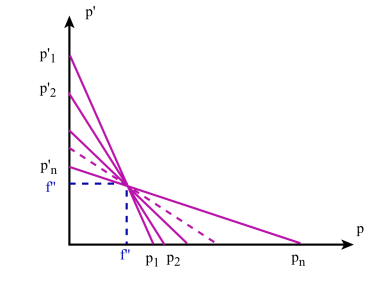
Une autre méthode graphique pour trouver f ' consiste à représenter les distances p et p' respectivement suivant les axes Ox et Oy et à joindre par un segment de droite les couples \((p_n, p'_n)\).
En effet si p et p' sont des distances : pour chaque couple \((p_n, p'_n)\) nous avons la relation en grandeurs (et non pas en valeurs algébriques) :
\(\frac1{p_n}+\frac1{p'_n}=\frac1{f'}\)
Si nous cherchons l'équation de la droite qui joint un couple de points \((p_n, p'_n)\) nous obtenons :
\(y=-\frac{p'_n}{p_n}~x+p'_n\)
or \(~\frac1{p_n}=\frac1{f'}-\frac1{p'_n}=\frac{p'_n~-~f'}{p'_n~.~f'}\)
\(p_n=\frac{p'_n~.~f'}{p'_n~-~f'}\)
soit en remplaçant : \(~y=\frac{f'~-~p'_n}{f'}~x+p'_n~~~~~~(1)\)
\(x=(y~-~p'_n)~\frac{f'}{f'~-~p'_n}~~~~~~(2)\)
Si maintenant nous faisons :
x = f ' dans la relation (1) nous obtenons y = f '
y = f ' dans la relation (2) nous obtenons x = f '
quel que soit le couple de points \((p_n, p'_n)\)
L'ensemble du faisceau de segments de droite qui joignent les couples de points conjugués[3] \((p_n, p'_n)\) se coupent en un point de coordonnées f ' , f '.
D'où la méthode pour déterminer graphiquement la distance focale[4] de la lentille.
Simuler
L'animation didacticielle suivante illustre la détermination d'une distance focale par la méthode des points conjugués :