Méthode de Badal
applicable aux lentilles convergentes et divergentes
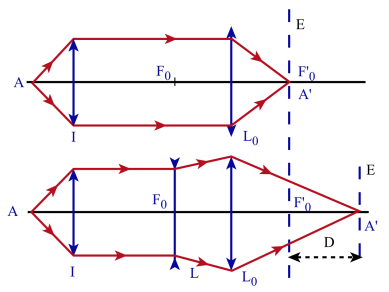
La lentille l donne d'un point objet[1] A une image[2] à l'infini (réglage par auto collimation par exemple). La lentille \(L_{\mathit0}\) de distance focale[3] \(f'_{\mathit0}\) connue est placée derrière l à une distance supérieure à sa distance focale \(f '_{\mathit0}\) (\(F_{\mathit0}\) est entre l et \(L_{\mathit0}\)). \(L_{\mathit0}\) donne alors une image A' de A dans le plan focal image E de \(L_{\mathit0}\) située en \(F'_{\mathit0}\).
On place alors la lentille L dont on cherche à déterminer la distance focale f ' dans le plan focal objet de \(L_{\mathit0}\). Pour obtenir une image nette A' on doit déplacer l'écran E d'une distance D et l'on a :
\(f'=-\frac{{f'}_{\mathit0}^2}{D}\)
déduite de la formule de Newton appliquée à la lentille \(L_{\mathit0}\).
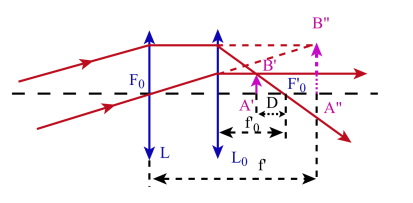
La figure ci-dessus est faite dans le cas d'une lentille L inconnue et convergente.
pour une lentille divergente, le déplacement D est positif et la distance focale image est négative
pour une lentille convergente, le déplacement D est négatif mais ne peut pas être supérieur à \(f'_{\mathit0}\) en valeur absolue : \(~f'>f'_{\mathit0}\)
Simuler
L'animation didacticielle suivante illustre la détermination d'une distance focale par la méthode de Badal :