Description optique de l'œil.
Dioptre cornéen antérieur
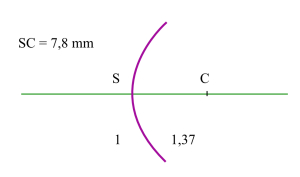
la vergence du dioptre est :
\(C_{\mathit1}=\frac{n_{\mathit2}~-~n_{\mathit1}}{\overline{SC}}=\frac{0,37}{7,8.10^{-3}}=47,4~\mathrm{dioptries}\)
c'est donc un dioptre convergent[1].
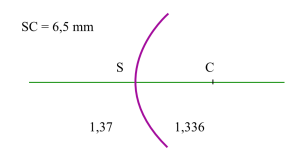
Dioptre cornéen postérieur
Dioptre cristallin antérieur
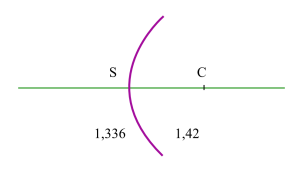
Le cristallin possède une structure feuilletée équivalente à une structure de dioptres d'indice très proches dont l'indice de réfraction moyen est égal à 1,42.
Son rayon moyen au repos vaut 10 mm.
La vergence est donnée par :
\(C_{\mathit3}=\frac{1,42-1,336}{10.10^{-3}}=8,4~\mathrm{dioptries}\)
c'est un dioptre convergent[1] dont la vergence varie lors de l'accommodation puisque SC diminue et donc C3 augmente.
Dioptre cristallin postérieur
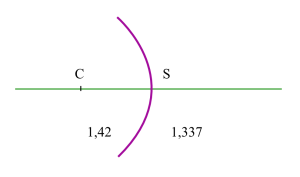
\(\overline{SC}=-6~\mathrm{mm}\)
La vergence est donnée par :
\(C_{\mathit4}=\frac{1,337-1,42}{-6.10^{-3}}=13,8~\mathrm{dioptries}\)
c'est un dioptre convergent[1].
la vergence totale du cristallin est donc de l'ordre de 22 dioptries.
La vergence de l'ensemble cornée + cristallin est donc de l'ordre de 60 dioptries.
L'axe visuel ou axe optique joint la fovéa au centre optique C de l'oeil et fait un angle de 5° environ avec l'axe géométrique.
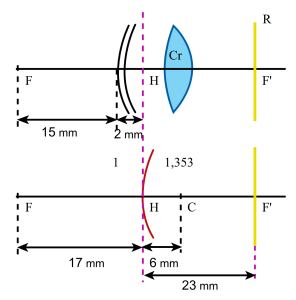
Oeil réduit
Les rayons issus d'un objet[2] et formant l'image[3] rétinienne sont paraxiaux[4] et les conditions de l'approximation de Gauss[5] sont satisfaites ; on peut ainsi définir les éléments cardinaux de l'oeil.
La distance focale image f ' vaut 23 mm et la distance focale objet vaut 17 mm. Pour l'oeil normal au repos le foyer image[6] F ' est sur la rétine et le foyer objet[6] F est à 15 mm en avant de la cornée.
De ces positions et des dimensions de l'oeil il résulte que la distance HH' est environ 0,3 mm ainsi que pour la distance NN' entre les points nodaux, si bien que l'on pourra confondre H et H', ainsi que N et N'.
On pourra ainsi dire que :
l’œil est équivalent à un dioptre unique de sommet S (position commune de H et H'), de centre C (ou centre optique confondu avec N et N') de 6 mm de rayon de courbure. C'est ce que l'on appelle l’œil réduit ou œil réduit de Listing.
Le rayon incident se propage dans l'air d'indice 1 tandis que le rayon réfracté se propage dans un milieu d'indice 1,353 donné par :
\(n=-\frac{\overline{SF'}}{\overline{SF}}=-\frac{23}{-17}=1,353\)