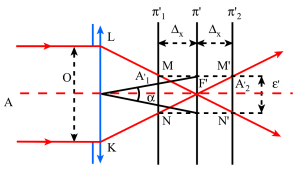
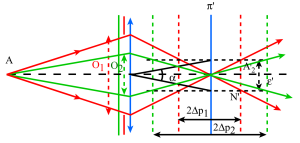
a- Champ axial pour un instrument objectif
Le champ axial ou champ en profondeur est mesuré par le segment axial entre les extrémités duquel doit se trouver un point objet[1] pour que son image[2] soit nette.
Nous étudierons par exemple le cas d'un objectif photographique. L'image réelle[3] est recueillie sur la plaque photographique.
La mise au point consiste à amener le plan du film photographique dans le plan \(p'\) conjugué d'un plan objet \(p\) (on met au point sur le plan objet).
La profondeur de champ, dans l'espace image[4], constituée par la distance séparant les limites entre lesquelles on peut déplacer le plan \(p'\) sans perdre la netteté des points du plan objet \(p\) est appelée latitude de mise au point. La profondeur de champ, dans espace objet[5], constituée par la distance séparant les limites entre lesquelles on peut déplacer le plan \(p\) tout en conservant la netteté des points dans le plan image fixe \(p'\) est appelée profondeur de netteté.
Nous supposerons que dans le plan image, l'image d'un point soit une petite tache circulaire de diamètre \(\varepsilon'\) .Cette image sera d'autant plus nette que \(\varepsilon'\) sera plus petit. Nous supposerons que le grain du film photographique n'intervient pas dans la définition de la netteté et que seul le fait que le faisceau[6] émergent converge en avant ou en arrière du plan du film en découpant sur ce plan image une tache circulaire de diamètre \(\varepsilon'\) contribue au défaut de netteté (défaut de mise au point).
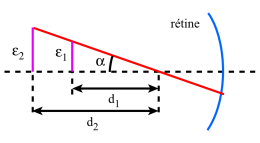
L'impression de plus ou moins grande netteté dépend de l'image rétinienne dont le diamètre est proportionnel à l'angle \(\alpha\).
Deux taches de diamètre \(\varepsilon_{\mathit1}\) et \(\varepsilon_{\mathit2}\) observées aux distances \(d_{\mathit1}\) et \(d_{\mathit2}\) seront vues sous le même angle \(\alpha\) produisant le même effet de netteté.
La netteté linéaire dépendra donc de la distance d'observation alors que la netteté angulaire ne dépendra que de l'oeil. On a : \(\varepsilon'=\alpha~.~d\). La valeur adoptée pour \(\alpha\) conduisant à une grande netteté est : \(\alpha=l'=3.10^{-4}~\mathrm{rd}\). D'autre part, pour que la perspective soit respectée, il faut que la photographie soit observée sous un angle égal au diamètre apparent de l'objet vu du point nodal de l'objectif, angle égal au diamètre apparent de l'image vu du point nodal image de l'objectif.
On définit ainsi la distance d'observation orthoscopique qui est la distance d'observation qui respecte la perspective et qui correspond approximativement à la distance entre l'objectif et le plan du film photographique. Lorsque l'objet est éloigné la distance orthoscopique est \(f\) et : \(\varepsilon'=\alpha~.~f\).
Lorsque la distance focale[7] est courte (appareils de petit format) on pourra cependant faire une observation orthoscopique soit en utilisant une loupe de même focale que l'objectif soit en observant un agrandissement de l'épreuve (grandissement[8] \(\gamma\)) conduisant à une distance orthoscopique \(\gamma~.~f\).
Dans ce qui suit nous ferons l'approximation consistant à assimiler l'objectif à une lentille mince[9] en confondant le plan de celle-ci avec les plans principaux et nodaux, le diaphragme d'ouverture et les pupilles d'entrée et de sortie.
Latitude de mise au point.
Cas où l'objet est très éloigné.(A à l'infini)
La position correcte du plan du film doit se situer dans le plan focal image \(\pi'\) de l'objectif. \(~\varepsilon'=\alpha.f\)
Si O est le diamètre du diaphragme d'ouverture, le nombre d'ouverture de l'objectif est : \(~N=\frac fO\)
Considérons le faisceau convergent[6] en \(F'\) et deux plans \(~\pi'_{\mathit1}~\) et \(~\pi'_{\mathit2}~\) distants de \(\Delta x\) de part et d'autre du plan focal \(\pi'\) et tels que le faisceau découpe sur ces plans des tâches de diamètre égal à \(\varepsilon'\). \(~\Delta x\) étant supposé petit par rapport à la distance focale[7] \(~f~\), on pourra admettre que la netteté linéaire est sensiblement la même dans les plans \(~\pi'_{\mathit1}~\), \(~\pi'~\) et \(~\pi'_{\mathit2}~\).
La distance \(A'_{\mathit1}A'_{\mathit2}=2\Delta x\) représente la profondeur de foyer.
En considérant les triangles \(LKF'\) et \(MNF'\) : \(~\frac{\varepsilon'}O=\frac{\Delta x}f~\) soit : \(~2\Delta x=2~\varepsilon'~\frac fO=2.\varepsilon'.N=2.\alpha f.N\)
La profondeur de foyer, distance qui sépare les positions extrêmes entre lesquelles l'image d'un objet éloigné est suffisamment nette, est proportionnelle au nombre d'ouverture N de l'objectif et à sa distance focale.
On voit sur la figure ci-contre qu'un déplacement du film photographique au voisinage du plan de mise au point \(~\pi'~\) entraînera une altération de la mise au point d'autant plus importante que l'ouverture de l'objectif photographique sera plus importante.
Donc pour effectuer une bonne mise au point il vaut mieux opérer à pleine ouverture.
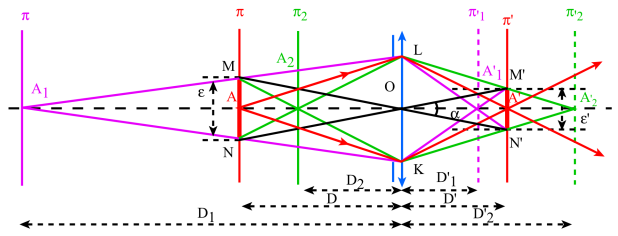
Profondeur de netteté dans espace objet[5].
Nous recherchons les positions \(A_{\mathit1}\) et \(A_{\mathit2}\) pour lesquelles les images sont nettes dans le plan fixe de la plaque photographique. Les faisceaux issus de \(A_{\mathit1}\) et \(A_{\mathit2}\) convergent[6] en \(A'_{\mathit1}\) et \(A'_{\mathit2}\) et découpent dans le plan \(\pi'\) une tâche de diamètre \(M'N'\) égale à la netteté linéaire : \(~\varepsilon'=\alpha~.~OA'=\alpha~.~D'~\) correspondant à la vision orthoscopique à la distance \(D'\).
Dans espace objet[5] les faisceaux issus de \(A_{\mathit1}\) et \(A_{\mathit2}\) découpent dans le plan objet \(\pi\) une tache de diamètre \(MN\) telle que : \(MN=\varepsilon=\alpha~.~D~\) et l'on a : \(~\varepsilon'=\gamma.\varepsilon~\) où \(\gamma\) est le grandissement[8] linéaire pour les plans \(~\pi~\) et \(~\pi'~\).
En utilisant les triangles semblables \(LKA_{\mathit1}\) et \(MNA_{\mathit1}\) d'une part et \(LKA_{\mathit2}\) et \(MNA_{\mathit2}\) d'autre part :
\(\frac{\varepsilon}O=\frac{\alpha D}O=\frac{D_{\mathit1}~-~D}{D_{\mathit1}}=\frac{D~-~D_{\mathit2}}{D_{\mathit2}}\)
\(\frac{\alpha}O=\frac{\alpha N}f=\frac1D-\frac1{D_{\mathit1}}=\frac1{D_{\mathit2}}-\frac1D\)
\(\frac{2\alpha}O=\frac{2\alpha N}f=\frac1{D_{\mathit2}}-\frac1{D_{\mathit1}}\)
\(\frac1D=\frac1{2}~\Big(\frac1{D_{\mathit1}}+\frac1{D_{\mathit2}}\Big)\)
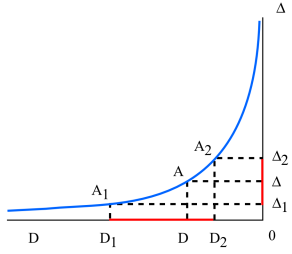
soit en introduisant la notion de proximité ou profondeur dioptrique :
\(\Delta=\frac1D~\) (hyperbole équilatère)
on obtient :
\(\frac{\alpha N}f=\Delta-\Delta_1=\Delta_2-\Delta\)
\(\frac{2\alpha N}f=\Delta_2-\Delta_1\)
\(\Delta=\frac1{2}~(\Delta_1+\Delta_2)\)
lorsque l'objectif travaille avec une distance de mise au point \(D\) et une ouverture \(N\), la profondeur dioptrique de netteté \(~\Delta_2-\Delta_1~\) est proportionnelle au nombre d'ouverture \(N\) et ne dépend pas de la mise au point. La profondeur de netteté \(AA_{\mathit1}\) est plus grande au delà de \(A\) que la profondeur de netteté \(AA_{\mathit2}\) en deçà de \(A\).
On observe que : La profondeur de netteté est d'autant plus grande que le diaphragme est plus réduit (N grand) et que l'objet est plus éloigné (\(\alpha\) petit).
On comprend pourquoi il faut mettre au point à pleine ouverture et ensuite réduire le diaphragme pour que le champ de netteté soit suffisamment profond.
lorsque la plaque sensible est dans le plan focal de l'objectif, \(~D' = f~\), \(D\) est infini et
\(~\frac1{D_{\mathit2}}=\frac{\alpha}O=\frac{\alpha N}f~\) soit : \(~H=\frac O{\alpha}=\frac f{\alpha N}\)
\(H\) est appelée distance hyperfocale et au delà de cette distance les images correspondantes sont au point sur la plaque photographique placée dans le plan focal image de l'objectif. On peut exprimer \(H\) de façon générale en fonction de \(D_{\mathit1}\) et \(D_{\mathit2}\) : \(H=\frac f{\alpha N}=\frac{2.D_{\mathit1}.D_{\mathit2}}{D_{\mathit1}~-~D_{\mathit2}}\)
Si l'on veut une photographie nette d'objets situés entre des distances comprises entre \(D_{\mathit1}\) et \(D_{\mathit2}\) , il suffira de mettre au point à une distance \(D=\frac{2.D_{\mathit1}.D_{\mathit2}}{D_{\mathit1}~+~D_{\mathit2}}\)
On retiendra simplement qu'il faut mettre au point sur un plan intermédiaire en deçà du milieu des plans extrêmes.