Pouvoir séparateur [Qualités d'un instrument]

Pouvoir séparateur

Le pouvoir séparateur exprime l'aptitude qu'a un instrument d'optique à séparer des détails rapprochés angulairement ou linéairement. Nous définirons ainsi une limite angulaire ou linéaire de séparation ( ou de résolution) dont l'inverse sera appelé pouvoir séparateur ou pouvoir de résolution angulaire ou linéaire.

Un instrument parfait donne d'un point A une figure de diffraction formée d'une tâche centrale (disque d'Airy) dont le centre est l'image^[1] géométrique A' du point A entourée d'anneaux dont l'influence est négligeable en première approximation.

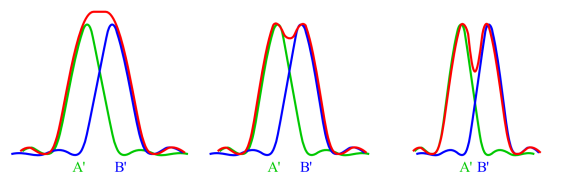
Deux points objets A et B voisins dans un plan de front^[2] objet ont des images d'Airy de centre A' et B'. Ces images sont séparées si elles n'empiètent pas trop l'une sur l'autre de telle sorte qu'il existe un minimum d'éclairement suffisamment net entre les deux maximum A' et B'.

Le critère de Rayleigh fixe conventionnellement la limite de résolution pour un instrument parfait :

Deux images d'Airy sont séparées lorsque la distance A'B' de leurs centres est supérieure à leur rayon commun y', autrement dit la limite de résolution est atteinte lorsque le premier minimum nul d'une figure de diffraction coïncide avec le maximum central de l'autre.

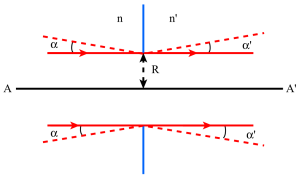
Le critère de Lord Rayleigh détermine la limite angulaire ou linéaire de résolution dans l'espace image, par A'B' ou \(~\alpha'~\), aussi bien que dans l'espace objet^[3] par AB et \(~\alpha~\) avec :

\(n~.~AB~.~\sin~u=n'~.~A'B'~.~\sin~u'\)

\(n~.~R_{\mathit0}~.~\alpha=n'~.~A'B'~.~\sin~u'\)

\(n~.~y~.~\sin~u=n'~.~R'_{\mathit0}~.~\alpha'\)

\(n~.~R_{\mathit0}~.~\alpha=n'~.~R'_{\mathit0}~.~\alpha'\)

Considérons le cas idéal où le système centré est réduit à un diaphragme circulaire D de rayon R séparant deux milieux d'indices n et n'.

Soit un point A situé sur l'axe ou au voisinage de l'axe; le système afocal donne de ce point une tache image d'Airy de rayon angulaire :

\(\alpha'=\frac{1,22~\lambda'}{2R}=\frac{0,6~\lambda'}{R}=\frac{0,6~\lambda_{\mathit0}}{n'R}\)

où \(~\lambda'~\) et \(~\lambda_{\mathit0}~\) sont les longueurs d'onde de la radiation utilisée dans le milieu d'indice n' et dans le vide.

Le rayon angulaire de la tache fictive objet est (selon le principe du retour inverse de la lumière) :

\(\alpha=\frac{0,6~\lambda}{R}=\frac{0,6~\lambda_{\mathit0}}{nR}\)

où \(\lambda\) est la longueur d'onde de la radiation utilisée dans le milieu d'indice n.

Les limites de résolution dans les espaces objet et image sont données par :

\(n~.~R~.~\alpha=n'~.~R'~.~\alpha'=0,6~\lambda_{\mathit0}\)

\(0,6~\lambda_{\mathit0}\) est l'invariant de la condition d'aplanétisme^[4].

Notes

Image
On appelle image d'un objet par un système optique, l'ensemble des images des points de l'objet.
On appelle image d'un point, la zone de convergence des rayons, après traversée du système optique (image réelle) ou la zone d'où les rayons semblent provenir (image virtuelle). Lorsque cette zone se réduit à un point, le système est dit stigmatique.
En pratique, l'image ressemble à l'objet (sinon le système ne présente pas d'intérêt), elle peut être
- agrandie : plus grande que l'objet ( |grandissement| >1) ;
- rapetissée : plus petite que l'objet ( |grandissement| <1) ;
- droite : dans le même sens que l'objet (grandissement >0) ;
- renversée : dans le sens contraire à l'objet (grandissement <0) ;
- déformée : un système qui déforme parce qu'il n'a pas le même grandissement dans différentes directions provoque une anamorphose (ex : glace déformante) ;
- floue
Plan de Front
Etant donné un système optique centré, on appelle plan de front tout plan perpendiculaire à l'axe principal qui est un axe de symétrie de révolution pour le système optique.
Exemple : sur cette figure, l'objet \(AB\) et l'image \(A'B'\) sont situés dans des plans de front.
Espace Objet
Espace Objet Réel
L'espace objet réel s'étend en deçà de la face d'entrée du système optique. Un objet situé dans cet espace hachuré est réel : les rayons passent vraiment par le point A.
Espace Objet Virtuel
L'espace objet virtuel s'étend au delà de la face d'entrée du système optique. Un objet situé dans cet espace grisé est virtuel : c'est le prolongement des rayons en aval de la face d'entrée, qui convergent au point A.
Aplanétisme
Un système centré est dit aplanétique lorsqu'on a stigmatisme dans un plan de front et que les points images de ce plan se situent dans un plan de front .
C'est à dire que, si A et A' sont conjugués, quelque soit B contenu dans le plan perpendiculaire à l'axe principal et passant par A, le point B', image de B, appartient au plan de front de A'.