Addition vectorielle
Définition :
La somme de deux vecteurs libres \(\overrightarrow{U}\) et \(\overrightarrow{V}\), notée \(\overrightarrow{U} + \overrightarrow{V}\), est un vecteur libre \(\overrightarrow{W}\), obtenu par la "règle du parallélogramme".
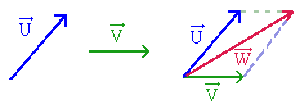
\(\overrightarrow{W} = \overrightarrow{U} + \overrightarrow{V}\)
Propriété :
L'addition vectorielle est une loi de composition interne et possède les propriétés suivantes :
Associativité : \(\bigg(\overrightarrow{U} + \overrightarrow{V}\bigg) + \overrightarrow{W} = \overrightarrow{U} + \bigg( \overrightarrow{V} + \overrightarrow{W}\bigg)\)
Commutativité :\(\overrightarrow{U} + \overrightarrow{V} = \overrightarrow{V} + \overrightarrow{U}\)
Élément neutre : \(\overrightarrow{U} + \overrightarrow{0} = \overrightarrow{0} + \overrightarrow{U} = \overrightarrow{U}\)(\(\overrightarrow{0}\) vecteur nul)
Élément symétrique : \(\overrightarrow{U} + \bigg( - \overrightarrow{U} \bigg) = \overrightarrow{0}\) (\(-\overrightarrow{U}\) vecteur opposé de \(\overrightarrow{U}\))
Applications
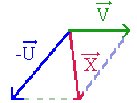
Étant donné deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\) il existe un unique vecteur \(\overrightarrow{X}\) tel que :
\(\overrightarrow{U} + \overrightarrow{X} = \overrightarrow{V} \Rightarrow \overrightarrow{X} = \overrightarrow{V} - \overrightarrow{U} = \overrightarrow{V} + \bigg( - \overrightarrow{U} \bigg)\)
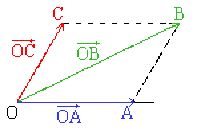
En représentant les vecteurs \(\overrightarrow{U}\), \(\overrightarrow{V}\) et \(\overrightarrow{W}\) respectivement par \(\overrightarrow{OC}\), \(\overrightarrow{OA}\) et \(\overrightarrow{OB}\) alors l'addition vectorielle \(\overrightarrow{W} = \overrightarrow{U} + \overrightarrow{V}\) conduit à :
\(\overrightarrow{OB} = \overrightarrow{OC} + \overrightarrow{OA} \Leftrightarrow \overrightarrow{OC} = \overrightarrow{OB} - \overrightarrow{OA}\)
or comme \(\overrightarrow{OC} = \overrightarrow{AB}\) on en déduit, quels que soient les points \(O\), \(A\) et \(B\) :
\(\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = \overrightarrow{AO} + \overrightarrow{OB}\) (Relation de Chasles)
Cas particulier :
Les trois points \(O\), \(A\) et \(B\) sont alignés sur une droite de vecteur unitaire \(\overrightarrow{u}\). Si les mesures algébriques des vecteurs \(\overrightarrow{AB}\), \(\overrightarrow{OA}\) et \(\overrightarrow{OB}\) sont notées \(\overline{AB}\), \(\overline{OA}\) et \(\overline{OB}\) alors : \(\overrightarrow{AB} = \overline{AB} ~\vec{u}\) ; \(\overrightarrow{OA} = \overline{OA} ~\vec{u}\) ; \(\overrightarrow{OB} = \overline{OB} ~\vec{u}\)
et nous obtenons la relation de Chasles pour les mesures algébriques :
\(\overline{AB} = \overline{OB} - \overline{OA} = \overline{AO} + \overline{OB}\)