Barycentre
Les points considérés appartiennent au plan ou à l'espace. Un point \(A_{i}\) affecté d'un réel \(\alpha_i,\)noté \((A_i, \alpha_i),\)est appelé point pondéré (point massif en physique quand \(\alpha_i > 0\) représente une masse).
Définition :
Le point \(G\) est appelé le barycentre, de n points pondérés \((A_1, \alpha_{1}), (A_2, \alpha_2), ..., (A_n, \alpha_n)\) si :
\(\displaystyle{\sum_{i = 1}^{n} \alpha_{i} \ne 0}\) et \(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} ~\overrightarrow{GA_{i}}= \overrightarrow{0}}\)
Pour un point \(O\) arbitraire, nous avons :
\(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} ~\overrightarrow{GA_{i}}= \sum_{i = 1}^{n} ~\alpha_{i} ~\bigg(\overrightarrow{OA_{i}}- \overrightarrow{OG} \bigg) = \sum_{i = 1}^{n} ~\alpha_{i} ~\overrightarrow{OA_{i}} - \bigg( \sum_{i = 1}^{n} ~\alpha_{i} \bigg) ~\overrightarrow{OG} = \overrightarrow{0}}\)
\(\overrightarrow{OG} = \frac{\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} ~\overrightarrow{OA_{i}}}}{\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i}}}\)
Coordonnées du barycentre : Dans l'espace muni d'un repère \(\bigg(O, \vec{i}, \vec{j}, \vec{k} \bigg)\), en notant \((x_i; y_i; z_i)\) les coordonnées du point pondéré \((A_i, \alpha_i)\) et \((x_G; y_G; z_G)\) celles de \(G\), alors :
\(x_G = \frac{\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} ~x_{i}}}{\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i}}} ;~ y_G = \frac{\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} ~y_{i}}}{\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i}}} ; ~ z_G = \frac{\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} ~z_{i}}}{\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i}}}\)
Exemple : Détermination des coordonnées du barycentre
On donne trois points dans un repère orthonormé \(\bigg(O, \vec{i},\vec{j},\vec{k} \bigg)\):
\(A (-3,1,2) ;~ B(-2,-1,1) ;~ C(0,3,-3)\)
Calculer les coordonnées \((x_G,y_G,z_G)\) du barycentre \(G\) de ces trois points pondérés respectivement des coefficients \(2\),\(-1\) et \(1\).
Calculons \(\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i} = 2-1+1 = 2 \ne 0}\), d'où
\(x_G = \frac{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i} ~x_{i}}}{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i}}} = \frac{1}{2} \bigg(2\bigg(-3\bigg) + \bigg(-1\bigg)\bigg(-2\bigg) + \bigg(1\bigg)\bigg(0\bigg)\bigg) = -2\)
\(y_G = \frac{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i} ~y_{i}}}{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i}}} = \frac{1}{2} \bigg(2\bigg(1\bigg) + \bigg(-1\bigg)\bigg(-1\bigg) + \bigg(1\bigg)\bigg(3\bigg)\bigg) = 3\)
\(z_G = \frac{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i} ~z_{i}}}{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i}}} = \frac{1}{2} \bigg(2\bigg(2\bigg) + \bigg(-1\bigg)\bigg(1\bigg) + \bigg(1\bigg)\bigg(-3\bigg)\bigg) = 0\)
donc \(G ~(-2,3,0)\) coordonnées du barycentre
Définition :
Le barycentre de \(n\) points pondérés \((A_1, \alpha_1), (A_2, \alpha_2), ..., (A_n, \alpha_n)\) avec \(\alpha \ne 0\), est appelé isobarycentre des \(n\) points \(A_1, A_2, ..., A_n\).
Exemple :
On donne trois points dans un repère orthonormé \(\bigg(O, \vec{i},\vec{j},\vec{k} \bigg)\):
\(A (-3,1,2) ;~ B(-2,-1,1) ;~ C(0,3,-3)\)
Calculer les coordonnées \((x'_G,y'_G,z'_G)\) de l'isobarycentre \(G'\) de ces trois points pondérés respectivement des coefficients \(\alpha_{A}=\alpha_{B} = \alpha_{C} = 1\).
Puisque \(\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i} = 1+1+1 = 3 }\), nous obtenons :
\(x'_G = \frac{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i} ~x_{i}}}{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i}}} = \frac{1}{3} \bigg(-3-2+0\bigg) = -\frac{5}{3}\)
\(y'_G = \frac{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i} ~y_{i}}}{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i}}} = \frac{1}{3} \bigg(1-1+3\bigg) = 1\)
\(z'_G = \frac{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i} ~z_{i}}}{\displaystyle{\sum_{i = 1}^{3} ~\alpha_{i}}} = \frac{1}{3} \bigg(2+1-3\bigg) = 0\)
donc \(G ~(-5/3,1,0)\) coordonnées de l'isobarycentre
Propriété :
Soit \((A_1, \alpha_1), (A_2, \alpha_2), ..., (A_n, a_n)\) \(n\) points pondérés :
Si \(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \ne 0}\)
Pour tout point \(M\), on a :
\(\alpha_{1} \overrightarrow{MA_{1}} + \alpha_{2} \overrightarrow{MA_{2}} + ... + \alpha_{n} \overrightarrow{MA_{n}} = \bigg( \alpha_{1} + \alpha_{2} +... +\alpha_{n} \bigg)\overrightarrow{MG}\)
\(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{MA_{i}}} = \bigg( \displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \bigg) \overrightarrow{MG}}\) \(\qquad\) (voir la démonstration ci dessous)
pour tout \(k \in \mathbb{R}^{*}\), les points pondérées \((A_1, \alpha_1), (A_2, \alpha_2), ..., (A_n, \alpha_n)\)
et \((A_1, k\alpha_1), (A_2, k\alpha_2), ..., (A_n, k\alpha_n)\) ont même barycentre car
\(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{GA_{i}}} = \overrightarrow{0} \Leftrightarrow \displaystyle{\sum_{i = 1}^{n} ~\big(k \alpha_{i}\big) \overrightarrow{GA_{i}}} = \overrightarrow{0}\) Invariance du barycentre
Démonstration :
\(\begin{array}{lll} \displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{MA_{i}}} & = \alpha_{1} \overrightarrow{MA_{1}} + \alpha_{2} \overrightarrow{MA_{2}} + ... + \alpha_{n} \overrightarrow{MA_{n}} \\ & = \alpha_{1} \bigg(\overrightarrow{MG} + \overrightarrow{GA_{1}}\bigg) + \alpha_{2} \bigg(\overrightarrow{MG} + \overrightarrow{GA_{2}}\bigg) + ... + \alpha_{n} \bigg(\overrightarrow{MG} + \overrightarrow{GA_{n}}\bigg) \\ & =\big(\alpha_{1} + \alpha_{2}+ ... + \alpha_{n} \big)\overrightarrow{MG} + \alpha_{1} \overrightarrow{GA_{1}} + \alpha_{2} \overrightarrow{GA_{2}} + ... + \alpha_{n} \overrightarrow{GA_{n}} \\ & = \displaystyle{ \bigg( \sum_{i = 1}^{n} ~\alpha_{i} \bigg) \overrightarrow{MG}} + \displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{GA_{i}}} = \displaystyle{ \bigg( \sum_{i = 1}^{n} ~\alpha_{i} \bigg) \overrightarrow{MG}} \end{array}\)
puisque par définition du barycentre : \(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{GA_{i}}} = \overrightarrow{0}\)
Propriété :
Le barycentre \(G\) de \(n\) points ponderés est invariant quand on remplace \(p\) d'entre eux, par leur barycentre \(H\), affecté de la somme \(\displaystyle{\sum_{i = 1}^{p} ~\alpha_{i} \ne 0}\) de leur coefficient, \(G\) est alors le barycentre de :
\(\bigg( \displaystyle{H . \sum_{i = 1}^{p} ~\alpha_{i} \bigg)},\big(A_{p+1}, \alpha_{p+1} \big),..,\big(A_{n},\alpha_{n}\big)\)
Démonstration :
Si \(H\) est le barycentre des points pondérés \((A_1, \alpha_1), (A_2, \alpha_2), ..., (A_p, \alpha_p)\) alors :
\(\displaystyle{\sum_{i = 1}^{p} ~\alpha_{i} \overrightarrow{MA_{i}}} = \displaystyle{\bigg(\sum_{i = 1}^{p} ~\alpha_{i} \bigg)\overrightarrow{MH}}\)
Pour le cas particulier où \(M = G \Rightarrow \displaystyle{\sum_{i = 1}^{p} ~\alpha_{i} \overrightarrow{GA_{i}}} = \displaystyle{\bigg(\sum_{i = 1}^{p} ~\alpha_{i} \bigg)\overrightarrow{GH}}\)
Or \(G\) étant le barycentre des \(n\) points pondérés \((A_1, \alpha_1), (A_2, \alpha_2), ..., (A_n, \alpha_n)\) donc
\(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{GA_{i}}} = \overrightarrow{0} \Rightarrow \displaystyle{\sum_{i = 1}^{p} ~\alpha_{i} \overrightarrow{GA_{i}}} + \displaystyle{\sum_{i = p+1}^{n} ~\alpha_{i} \overrightarrow{GA_{i}}} = \displaystyle{\bigg(\sum_{i = 1}^{p} ~\alpha_{i} \bigg) ~\overrightarrow{GH}} + \displaystyle{\sum_{i = p+1}^{n} ~\alpha_{i} \overrightarrow{GA_{i}}} = \overrightarrow{0}\)
Comme \(\displaystyle{\bigg(\sum_{i = 1}^{p} ~\alpha_{i} \bigg) } + \displaystyle{\bigg(\sum_{i = p+1}^{n} ~\alpha_{i} \bigg)} \ne 0\) l'égalité précédente prouve que \(G\) est le barycentre des points pondérés : \(\bigg( \displaystyle{H . \sum_{i = 1}^{p} ~\alpha_{i} \bigg)},\big(A_{p+1}, \alpha_{p+1} \big),..,\big(A_{n},\alpha_{n}\big)\)
Propriété :
Si \(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} = 0}\)
Pour tous points \(M\) et \(N\) :
\(\alpha_{1} ~\overrightarrow{MA_{1}} +\alpha_{2} ~\overrightarrow{MA_{2}} + ... + \alpha_{n} ~\overrightarrow{MA_{n}} = \alpha_{1} ~\overrightarrow{NA_{1}} +\alpha_{2} ~\overrightarrow{NA_{2}} +... + \alpha_{n} ~\overrightarrow{NA_{n}} = \textrm{cste}\)
\(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{MA_{i}}} =\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{NA_{i}}} = \textrm{cste}\)
Démonstration :
Pour \(M\) différent de \(N\), calculons : \(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{MA_{i}}} - \displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{NA_{i}}}\)
\(\begin{array}{lll} \displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{MA_{i}}} -\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{NA_{i}}} & = \alpha_{1} \overrightarrow{MA_{1}} + \alpha_{2} \overrightarrow{MA_{2}} + ... + \alpha_{n} \overrightarrow{MA_{n}} - \alpha_{1} \overrightarrow{NA_{1}} - \alpha_{2} \overrightarrow{NA_{2}} - ... - \alpha_{n} \overrightarrow{NA_{n}} \\ & = \alpha_{1} \bigg(\overrightarrow{MA_{1}} - \overrightarrow{NA_{1}}\bigg) + \alpha_{2} \bigg(\overrightarrow{MA_{2}} - \overrightarrow{NA_{2}}\bigg) + ... + \alpha_{n} \bigg(\overrightarrow{MA_{n}} - \overrightarrow{NA_{n}}\bigg) \\ & = \alpha_{1} \overrightarrow{MN} + \alpha_{2} \overrightarrow{MN} +...+\alpha_{n} \overrightarrow{MN} \\ & = (\alpha_{1} + \alpha_{2} + ... + \alpha_{n} ) \overrightarrow{MN} = \overrightarrow{0} \end{array}\)
puisque \(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i}} = 0\)
et \(\displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{MA_{i}}} = \displaystyle{\sum_{i = 1}^{n} ~\alpha_{i} \overrightarrow{NA_{i}}} = \textrm{cste}\)
Applications
En géométrie
L'isobarycentre \(G\) de deux points \(A\) et \(B\) se situe au milieu du segment \([AB]\).
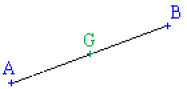
L'isobarycentre \(G\) de trois points \(A\), \(B\) et \(C\), non alignés, se trouve au centre de gravité du triangle \(ABC\), point de concours des trois médianes.
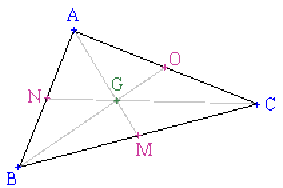
\(G\) point de concours des \(3\) médianes
\(AM\), \(BO\) et \(CN\) du triangle \(ABC\).
L'isobarycentre \(G\) de quatre points \(A\), \(B\), \(C\) et \(D\) , non coplanaires, est le centre de gravité du tétraèdre \(ABCD\), point de concours des quatre médianes et des trois droites joignant les milieux de deux arêtes opposées.
\(g_2\), \(g_3\) et \(g_4\) centre de gravité des triangles \(BCD\), \(ACD\), \(ABD\),\(ABC\)
\(G\) point de concours des quatre médianes \((Ag_1, Bg_2, Cg_3, Dg_4)\) et des trois droites \((EF, HI, JK)\) joignant les milieux de deux arêtes opposées.
\(\qquad\)
En Physique
Le barycentre \(G\) d'un système de \(n\) points matériels \(P_i\), de masse \(m_i\), est appelée centre de gravité ou centre d'inertie du système et défini par :
\(\overrightarrow{OG} = \frac{\displaystyle{\sum_{i = 1}^{n} ~m_{i} ~\overrightarrow{OP_{i}}}}{\displaystyle{\sum_{i = 1}^{n} ~m_{i}}} = \frac{1}{M}\displaystyle{\sum_{i = 1}^{n} ~m_{i} ~\overrightarrow{OP_{i}}}\)
avec \(M = m_1 + m_2 + ... + m_n\) masse totale du système
Le barycentre \(G\) d'un système matériel continu, se définit par :
\(\overrightarrow{OG} = \frac{\displaystyle{\textrm{lim}_{\Delta m_{i} \to 0}\sum_{i = 1}^{n} ~\Delta m_{i} ~\overrightarrow{OP_{i}}}}{\displaystyle{\sum_{i = 1}^{n} ~\Delta m_{i}}} = \frac{1}{M}~\int_{P \in \textrm{Syst\`eme}}~\overrightarrow{OP} \textrm{ dm}\)
avec \(\int_{P \in \textrm{Syst\`eme}}\) symbole d'intégration étendu au système matériel (courbe[1], surface[2], volume[3]).
Explication :
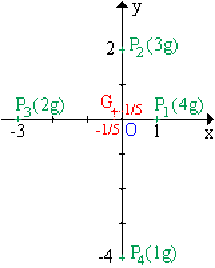
Quatre points massifs \(\big(P_i,m_i\big) : M = 4 + 3 + 2 + 1 = 10 \textrm{ g}\)
\(\overrightarrow{OG} =\frac{1}{M}\displaystyle{\sum_{i = 1}^{4} ~m_{i} ~\overrightarrow{OP_{i}}} = \frac{1}{M} \bigg(m_{1} ~\overrightarrow{OP_{1}} + m_{2} ~\overrightarrow{OP_{2}} + m_{3} ~\overrightarrow{OP_{3}} + m_{4} ~\overrightarrow{OP_{4}} \bigg)\)
Projection sur \(Ox\) :
\(x_{G} = \frac{1}{10} \bigg(\bigg(4\bigg)\bigg(1\bigg) + \bigg(2\bigg)\bigg(-3\bigg)\bigg) = - \frac{1}{5}\)
\(y_{G} = \frac{1}{10} \bigg(\bigg(3\bigg)\bigg(2\bigg) + \bigg(1\bigg)\bigg(-4\bigg)\bigg) = \frac{1}{5}\)
Centre de gravité \(G~(-1/5,1/5)\)