Multiplication d'un vecteur par un scalaire
Définition :
Le produit d'un vecteur \(\overrightarrow{V}\) par un scalaire \(\alpha\) est un vecteur, noté \(\alpha~ \overrightarrow{V}\), tel que :
sa direction est celle de \(\overrightarrow{V}\)
son sens : celui de \(\overrightarrow{V}\) si \(\alpha > 0\), celui \(- \overrightarrow{V}\) de si \(\alpha < 0\).
sa norme est égale au produit de celle de \(\overrightarrow{V}\) par la valeur absolue de \(\alpha\) : \(\big\Arrowvert \alpha \overrightarrow{V} \big\Arrowvert = | \alpha | \big\Arrowvert \overrightarrow{V} \big\Arrowvert\)
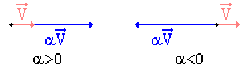
Exemple : Produit d'un vecteur par un scalaire
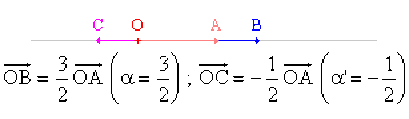
Propriété :
La multiplication d'un vecteur par un scalaire est une loi de composition externe vérifiant les propriétés :
Distributivité par rapport à l'addition des vecteurs : \(\alpha \bigg(\overrightarrow{U} + \overrightarrow{V}\bigg) = \alpha \overrightarrow{U} + \alpha \overrightarrow{V}\)
Distributivité par rapport à l'addition des scalaires : \(\bigg(\alpha + \beta \bigg) \overrightarrow{U} = \alpha \overrightarrow{U} + \beta \overrightarrow{U}\)
Associativité : \(\alpha \bigg(\beta \overrightarrow{U}\bigg) = \bigg( \alpha \beta \bigg) \overrightarrow{U}\)
Elément neutre : \(1 \overrightarrow{U} = \overrightarrow{U}\)
Applications
En géométrie
\(\qquad\) Détermination d'un point \(M\) sur une droite \(AB\) satisfaisant une relation vectorielle
Exemple : Position d'un point sur une droite
Etant donnés les points \(A\) et \(B\), déterminer un point \(M\) tel que : \(2~ \overrightarrow{MA} + \overrightarrow{MB} = 3~ \overrightarrow{AB}\)
En prenant l'origine en \(A\), exprimons \(\overrightarrow{AM}\) en fonction de \(\overrightarrow{AB}\):
\(\overrightarrow{MA} = - \overrightarrow{AM}\) et \(\overrightarrow{MB} = \overrightarrow{MA} + \overrightarrow{AB} = - \overrightarrow{AM} + \overrightarrow{AB}\)
d'où
\(2 ~\overrightarrow{MA} + \overrightarrow{MB} = 2\bigg(- \overrightarrow{AM}\bigg) + \bigg( -\overrightarrow{AM} + \overrightarrow{AB}\bigg) = -3 \overrightarrow{AM} + \overrightarrow{AB} = 3 \overrightarrow{AB}\)
\(-3~ \overrightarrow{AM} = 2 ~\overrightarrow{AB} \Rightarrow \overrightarrow{AM} = - \frac{2}{3}~ \overrightarrow{AB}\)

\(\qquad\) Combinaison linéaire de deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\) du plan.
Exemple : Combinaison linéaire de deux vecteurs
Étant donnés les deux vecteurs de base \(\overrightarrow{U}\) et \(\overrightarrow{V}\), déterminons le vecteur \(\overrightarrow{W}\), combinaison linéaire de \(\overrightarrow{U}\) et \(\overrightarrow{V}\): \(\overrightarrow{W} = 2 ~\overrightarrow{U} - 3~ \overrightarrow{V}\)
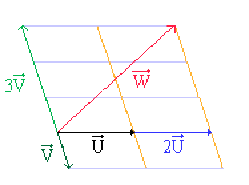
\(\qquad\) Reconnaître si trois vecteurs \(\overrightarrow{U}\), \(\overrightarrow{V}\) et \(\overrightarrow{W}\) sont coplanaires.
Exemple : Vecteurs coplanaires
Les vecteurs \(\overrightarrow{U} = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)\), \(\overrightarrow{V} = \left( \begin{array}{ccc} -2 \\ 1 \\ 3 \end{array} \right)\) et \(\overrightarrow{W} = \left( \begin{array}{ccc} 12 \\ -5 \\ -17 \end{array} \right)\) sont-ils coplanaires ?
Les vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\) n'étant pas colinéaires, cherchons si il existe deux réels \(a\) et \(b\) tels que \(\overrightarrow{W} =\alpha \overrightarrow{U} + \beta \overrightarrow{V}\)
or
\(\left( \begin{array}{ccc} 12 \\ -5 \\ -17 \end{array} \right) = \alpha \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right) + \beta \left( \begin{array}{ccc} -2 \\ 1 \\ 3 \end{array} \right) \Leftrightarrow \left \{ \begin{array}{lll} 12 = \alpha - 2 \beta \\ -5 = \beta \\ -17 = - \alpha + 3 \beta \end{array} \right. \Leftrightarrow \left \{ \begin{array}{lll} \alpha = 2 \\ \beta = -5 \end{array} \right.\)
\(\overrightarrow{W} = 2 \overrightarrow{U} - 5 \overrightarrow{V}\)
En Physique
\(\qquad\) Force \(\overrightarrow{F}\) subie sur une charge \(q\) dans un champ électrostatique \(\overrightarrow{E}\)
Exemple : Intéraction entre deux charges éléctriques
Une charge \(Q\) (\(>0\) ou \(<0\)) crée en un point \(M\) de l'espace un champ électrostatique \(\overrightarrow{E_{M}}\). Une charge ponctuelle \(q\) (\(>0\) ou \(<0\)) placée en \(M\) subira une force \(\overrightarrow{F_{M}}\) dont le sens dépendra des signes des charges \(Q\) et \(q\). Déterminer le sens de \(\overrightarrow{F_{M}}\).
Par définition : \(\overrightarrow{F_{M}} = q ~\overrightarrow{E_{M}}\)
Pour visualiser le champ et la force, cliquez sur la charge \(Q\).
\(1^{\textrm{er}}\textrm{ cas} : Q > 0, ~q > 0\)
\(2^{\textrm{\`eme}}\textrm{ cas} : Q > 0, ~q < 0\)
\(3^{\textrm{\`eme}}\textrm{ cas} : Q < 0, ~q > 0\)
\(4^{\textrm{\`eme}}\textrm{ cas} : Q < 0, ~q < 0\)
\(\qquad\) Conservation de la quantité de mouvement
Exemple : Conservation de la quantité de mouvement
Conservation de la quantité de mouvement lors du recul d'une arme à feu.
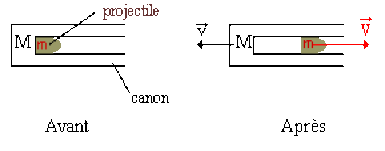
L'ensemble (arme - projectile) forme le système.
Avant la mise à feu : la quantité de mouvement est nulle.
Après la mise à feu : la somme des quantités de mouvements doit rester nulle.
d'où : \(M ~\overrightarrow{v} + m~ \overrightarrow{V} = \overrightarrow{0}\)
la vitesse de recul de l'arme à feu : \(\overrightarrow{v} = - \frac{m}{M}~ \overrightarrow{V}\)