Repère et coordonnées d'un point
Définition :
Un repère (ou repère cartésien) du plan est un triplet \(\bigg(O, \overrightarrow{e_{x}}, \overrightarrow{e_{y}} \bigg)\) où \(O\) est un point arbitrairement choisi comme origine et \(\bigg(\overrightarrow{e_{x}} , \overrightarrow{e_{y}} \bigg)\) deux vecteurs non colinéaires.
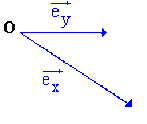
Un repère (ou repère cartésien) de l'espace est un quadruplet \(\bigg(O, \overrightarrow{e_{x}}, \overrightarrow{e_{y}}, \overrightarrow{e_{z}}\bigg)\) où \(O\) est un point arbitrairement choisi comme origine et \(\bigg(\overrightarrow{e_{x}} , \overrightarrow{e_{y}}, \overrightarrow{e_{z}}\bigg)\) trois vecteurs non coplanaires.
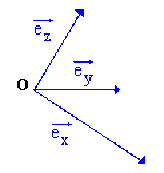
Le repère \(\bigg(O, \overrightarrow{e_{x}}, \overrightarrow{e_{y}}, \overrightarrow{e_{z}}\bigg)\) est dit repère cartésien orthogonal (ou rectangulaire) si les vecteurs \(\bigg(\overrightarrow{e_{x}} , \overrightarrow{e_{y}}, \overrightarrow{e_{z}}\bigg)\) sont deux à deux perpendiculaires.
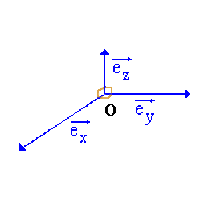
Le repère \(\bigg(O, \overrightarrow{e_{x}}, \overrightarrow{e_{y}}, \overrightarrow{e_{z}}\bigg)\) est dit repère cartésien orthonormal (ou orthonormé) si les trois vecteurs du repère cartésien orthogonal sont des vecteurs unitaires.\((\Arrowvert \overrightarrow{e_{x}} \Arrowvert=\Arrowvert \overrightarrow{e_{y}} \Arrowvert=\Arrowvert \overrightarrow{e_{z}}\Arrowvert = 1)\)
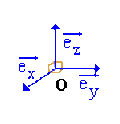
\(\qquad\)
On appelle coordonnées cartésiennes d'un point \(M\) de l'espace, les trois réels uniques \((x_M, y_M, z_M)\) définis respectivement par les relations :
\(\overrightarrow{OA} =x_{M} \overrightarrow{e_{x}}\); \(\overrightarrow{OB} =y_{M} \overrightarrow{e_{y}}\); \(\overrightarrow{OC} =z_{M} \overrightarrow{e_{z}}\) et \(\overrightarrow{OM} =x_{M} \overrightarrow{e_{x}} +y_{M} \overrightarrow{e_{y}} + z_{M} \overrightarrow{e_{z}}\) (le point \(A\), par exemple, est obtenu par projection de \(M\) sur un axe associé à \(\overrightarrow{e_{x}}\), parallèlement au plan défini par \(\overrightarrow{e_{y}}\) et \(\overrightarrow{e_{z}}\))
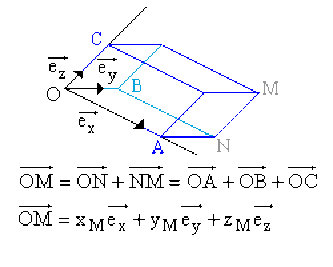
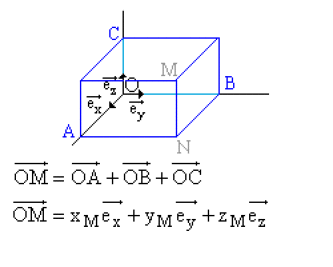
Un repère définit la position d'un point