Coordonnées d'un vecteur d'un repère
Définition :
Si \(\overrightarrow{OM}\) représente un vecteur \(\overrightarrow{U}\) de l'espace, on appelle \(x_M, y_M, z_M,\) les coordonnées (ou composantes) du vecteur \(\overrightarrow{U}\) dans la base \(\bigg(\overrightarrow{e_{x}} , \overrightarrow{e_{y}}, \overrightarrow{e_{z}}\bigg)\) :
On écrit :
\(\overrightarrow{U} = x_{M}\overrightarrow{e_{x}} + y_{M}\overrightarrow{e_{y}} +z_{M}\overrightarrow{e_{z}}\)
En Physique les composantes d'un vecteur sont souvent représentées par des lettres majuscules avec \(\bigg(\vec{i},\vec{j},\vec{k} \bigg)\) pour base cartésienne orthonormée, d'où :
\(\overrightarrow{U} = X \vec{i} + Y \vec{j} + Z \vec{k}\)
Propriété :
Soient les vecteurs \(\overrightarrow{U}(X,Y,Z)\) et \(\overrightarrow{V}(X',Y',Z')\) alors :
\(\overrightarrow{U} = \overrightarrow{V} \Leftrightarrow X = X' , Y = Y', Z = Z'\)
\(\overrightarrow{W_{1}} = \overrightarrow{U} + \overrightarrow{V} \Leftrightarrow \overrightarrow{W_{1}} (X'',Y'',Z'')\) avec \(X'' = X+X', ~Y'' = Y+Y', ~Z''=Z+Z'\)
\(\overrightarrow{W_{2}} =k \overrightarrow{U} ~(k \in \mathbb{R}) \Leftrightarrow \overrightarrow{W_{2}} (X''',Y''',Z''')\) avec \(X'''=k X,~~Y'''=k Y,~~Z'''=k Z\)
Etant donnés les points \(M(x,y,z)\) et \(N(x',y',z')\) dans \(\bigg(O,\vec{i},\vec{j},\vec{k}\bigg)\)
le vecteur \(\overrightarrow{MN}\) a pour composantes :
\(\overrightarrow{MN} = \overrightarrow{MO} + \overrightarrow{ON} = \overrightarrow{ON} - \overrightarrow{OM} = (x'-x,y'-y,z'-z)\)
la norme de \(\overrightarrow{MN}\) est définie par : \(\Arrowvert \overrightarrow{MN} \Arrowvert= \sqrt{(x'-x)^{2}+(y'-y)^{2}+(z'-z)^{2}}\)
le milieu \(I\) de \(MN\) a pour coordonnées : \(\overrightarrow{OI} = \frac{\overrightarrow {OM} + \overrightarrow{ON}}{2} = \bigg(\frac{x+x'}{2}, \frac{y+y'}{2}, \frac{z+z'}{2} \bigg)\)
Exemple :
Dans un repère cartésien orthonormé \(\bigg(O,\vec{i},\vec{j} \bigg)\), on donne les points \(A (1,2)\) et \(B(-3,4)\).
Déterminer les composantes du vecteur \(\overrightarrow{AB}\), la norme de ce vecteur, les coordonnées de \(I\), milieu de \(AB\).
Composantes de \(\overrightarrow{AB}\) :
\(\overrightarrow{AB} = \overrightarrow{AO} + \overrightarrow{OB} = \overrightarrow{OB} - \overrightarrow{OA} = \dbinom{-3}{4} - \dbinom{1}{2} = \dbinom{-4}{2}\)
\(\overrightarrow{AB} = -4 \vec{i} + 2 \vec{j}\)
Norme de \(\overrightarrow{AB}\)
\(\begin{array}{lll}\Arrowvert \overrightarrow{AB}\Arrowvert &= \sqrt{\Big(x_{B} - x_{A}\Big)^{2} + \Big(y_{B} - y_{A}\Big)^{2}} = \sqrt{\Big(-4\Big)^{2} + \Big(2\Big)^{2}} \\ & =\sqrt{20}= 2 \sqrt{5} \end{array}\)
Coordonnées de \(I\) milieu de \(AB\)
\(\overrightarrow{OI} = \frac{\overrightarrow{OA} + \overrightarrow{OB}}{2} = \frac{1}{2} \left[ \dbinom{1}{2} + \dbinom{-3}{4} \right]= \frac{1}{2} \dbinom{-2}{6} = \dbinom{-1}{3}\)
coordonnées de \(I\) : \(x_I = -1\) et \(y_I = 3\)
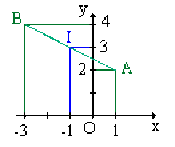
Une base définit un vecteur par ses composantes