Définitions
On appelle produit mixte entre trois vecteurs \(\overrightarrow{U}\), \(\overrightarrow{V}\) et \(\overrightarrow{W}\), le scalaire défini par :
\(\Big(\overrightarrow{U},\overrightarrow{V},\overrightarrow{W} \Big) = \Big(\overrightarrow{U} \wedge \overrightarrow{V} \Big) \cdot \overrightarrow{W}\)
Posons \(\overrightarrow{p} = \overrightarrow{U} \wedge \overrightarrow{V}\)
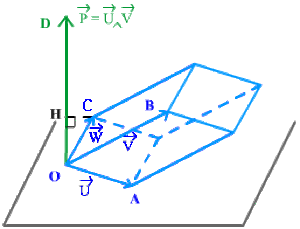
\(\Big(\overrightarrow{U},\overrightarrow{V},\overrightarrow{W}\Big) = \overrightarrow{p} \cdot \overrightarrow{W} = \overrightarrow{OD} \cdot \overrightarrow{OC}\)
Si \(H\) désigne la projection orthogonale de \(C\) sur \(OD\) alors :
\(\begin{array}{ll} \Big\arrowvert \Big(\overrightarrow{U},\overrightarrow{V},\overrightarrow{W} \Big) \Big\arrowvert &=\Big\Arrowvert \overrightarrow{OD} \cdot \overrightarrow{OC} \Big\Arrowvert = \Big\Arrowvert \overrightarrow{OD}\Big\Arrowvert ~\Big\Arrowvert \overrightarrow{OC} \Big\Arrowvert ~\Big\arrowvert\cos\Big(\overrightarrow{OD},\overrightarrow{OC}\Big)\Big\arrowvert \\ &= \Big\Arrowvert \overrightarrow{OD}\Big\Arrowvert~\Big\Arrowvert \overrightarrow{OH}\Big\Arrowvert \end{array}\)
avec \(\Big\Arrowvert\overrightarrow{OD}\Big\Arrowvert = \Big\Arrowvert\overrightarrow {U} \wedge \overrightarrow{V}\Big\Arrowvert\) aire du parallélogramme construit sur \(\Big(\overrightarrow{OA},\overrightarrow{OB}\Big)\) et donc :
\(\Big\arrowvert\Big(\overrightarrow{U},\overrightarrow{V},\overrightarrow{W} \Big)\Big\arrowvert\) : Volume du parallélépipède d'arêtes \(OA\), \(OB\) et \(OC\)
Dans la base orthonormée directe \(\Big(\vec{i},\vec{j},\vec{k} \Big)\) le produit mixte de trois vecteurs :
\(\overrightarrow{U} = U_{x} \vec{i} + U_{y} \vec{j} + U_{z} \vec{k}\)
\(\overrightarrow{V} = V_{x} \vec{i} + V_{y} \vec{j} + V_{z} \vec{k}\)
\(\overrightarrow{W} = W_{x} \vec{i} + W_{y} \vec{j} + W_{z} \vec{k}\)
s'exprime par le scalaire :
\(\begin{array}{ll} \Big(\overrightarrow{U},\overrightarrow{V},\overrightarrow{W} \Big) &=\Big( \overrightarrow{U} \wedge \overrightarrow{V}\Big) \cdot \overrightarrow{W} \\ &= \Big(U_{y}V_{z} - U_{z}V_{y} \Big) W_{x} +\Big(U_{z}V_{x} - U_{x}V_{z} \Big) W_{y} +\Big(U_{x}V_{y} - U_{y}V_{x} \Big) W_{z} \end{array}\)
Il est possible de retrouver ce résultat par le développement d'un déterminant d'ordre \(3\), dont les colonnes contiennent respectivement les composantes des vecteurs \(\overrightarrow{U}\), \(\overrightarrow{V}\) et \(\overrightarrow{W}\).
Démonstration :
Calcul du produit mixte des vecteurs \(\Big(\overrightarrow{U},\overrightarrow{V},\overrightarrow{W} \Big)\)
\(\overset{\begin{array}{lcr}\overrightarrow{U}~& \overrightarrow{V} &~\overrightarrow{W} \end{array}}{\left\arrowvert\begin{array}{rcl} U_{x} & V_{x} & W_{x} \\ U_{y} & V_{y} & W_{y} \\ U_{z} & V_{z} & W_{z} \end{array}\right\arrowvert}\)
Le déterminant d'ordre \(3\) peut se calculer avec la règle de Sarrus[1]
\(\Delta = U_{x}V_{y}W_{z} + V_{x}W_{y}U_{z} +U_{y}V_{z}W_{x} -U_{z}V_{y}W_{x} -U_{y}V_{x}W_{z} -U_{x}V_{z}W_{y}\)
\(\Delta = \Big(U_{y}V_{z} - U_{z}V_{y} \Big) W_{x} +\Big(U_{z}V_{x} - U_{x}V_{z} \Big) W_{y} +\Big(U_{x}V_{y} - U_{y}V_{x} \Big) W_{z}\)
Exemple : Calcul de produit mixte
Soit \(\overrightarrow{U}(3,1,2)\), \(\overrightarrow{V}(1,1,1)\) et \(\overrightarrow{W}(1,2,1)\). Calculer \(\Big(\overrightarrow{U},\overrightarrow{V},\overrightarrow{W} \Big)\).
Par définition du produit mixte : \(\Big(\overrightarrow{U},\overrightarrow{V},\overrightarrow{W} \Big) =\Big( \overrightarrow{U} \wedge \overrightarrow{V}\Big) \cdot \overrightarrow{W}\)
or
\(\overrightarrow{U} \wedge \overrightarrow{V} = \left[ \begin{array}{c} 3 \\ 1 \\ 2 \end{array} \right. \wedge \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right. = \left[ \begin{array}{c} 1 - 2\\ -(2-3) \\ 3-1 \end{array} \right. = \left[ \begin{array}{c} -1 \\ 1 \\ 2 \end{array} \right.\)
d'où
\(\Big(\overrightarrow{U} \wedge \overrightarrow{V}\Big) \cdot \overrightarrow{W} = \left[ \begin{array}{c} -1 \\ 1 \\ 2 \end{array} \right. \cdot \left[ \begin{array}{c} 1 \\ 2 \\ 1 \end{array} \right. = (-1)(1) + (1)(2) + (2)(1) = 3\)