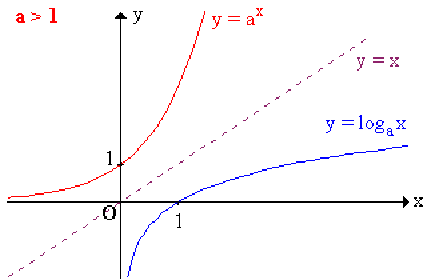Fonction exponentielle de x, dans la base a
Définition :
On appelle fonction exponentielle de base a \(\left(a \in \mathbb{R}_{+}^{\ast} - \{1\}\right)\), la fonction notée \(\exp_{a}\) (ou \(a^{x}\)), réciproque de \(\log_{a}\) :
\(\forall (x,y) \in \mathbb{R} \times \mathbb{R}_{+}^{\ast} \quad y= \exp_{a} x \Leftrightarrow x = \log_{a} y\)
Propriétés des fonctions \(\exp_{a}\) \((a \in \mathbb{R}_{+}^{\ast})\)
\(\forall a \in \mathbb{R}_{+}^{\ast},~ \forall x \in \mathbb{R} \quad \exp_{a} x = \textrm{e}^{x \ln a}\)
Démonstration :
\(x = \log_{a} \left(\exp_{a} x \right) = \frac{\ln \left(\exp_{a}x \right)}{\ln a}\)
\(\Leftrightarrow \ln \left(\exp_{a} x \right) = x \ln ~a\)
\(\Leftrightarrow \exp_{a} x = \textrm{e}^{x \ln ~a}\)
\(\forall a \in \mathbb{R}_{+}^{\ast}, \forall x \in \mathbb{R} \quad \exp_{a} x = a^{x}\)
Remarque :
La notation \(a^{x}\) a été définie pour :
\(a \in \mathbb{R}_{+}^{\ast}\) et \(x\) entiers ou fractionnaires \((\mathbb{N}, \mathbb{Z}, \mathbb{Q})\), positif ou négatif et pour \(a \ne 1\), nous avons :
\(\left.\begin{array}{ccc} \ln \left(a^{x}\right) = x \ln ~a \\ \ln \left(\exp_{a} x\right) = x \ln~a \end{array} \right \} \Rightarrow \exp_{a} x = a^{x}\)
on prolonge la notation \(a^{x}\) pour \(x \in \mathbb{R}\), en regardant \(a^{x}\) comme la limite commune vers laquelle tendent les deux suites de puissances de \(a\) ayant pour exposants les valeurs approchées de \(x\) à \(1/10\), \(1/100\), \(1/1000\), ... pris par défaut et par excés.
Exemple : Sachant que \(\sqrt{2} = \mathrm{1,4142...,}\) la valeur de \(3^{\sqrt{2}}\) sera la limite commune des deux suites
\(\begin{array}{llllllll} 3^{\tfrac{14}{10}} = \mathrm{4,6555367} & 3^{\tfrac{15}{10}} = \mathrm{5,1961524} \\ 3^{\tfrac{141}{100}} = \mathrm{4,706965} & 3^{\tfrac{142}{100}} = \mathrm{4,7589614} \\ 3^{\tfrac{1414}{1000}} = \mathrm{4,727695} & 3^{\tfrac{1415}{1000}} = \mathrm{4,7328918} \\ 3^{\tfrac{14142}{10000}} = \mathrm{4,7287339} & 3^{\tfrac{14143}{10000}} = \mathrm{4,7292535} \\\ldots & \ldots \\ \qquad 3^{\sqrt{2}} = \mathrm{4,7288044}\end{array}\)
La notation \(a^{x}\) sera préférée à \(\exp_{a} x\)
\(a^{0} = 1\)
\(\forall x \in \mathbb{R} \qquad 1^{x} = 1\)
\(\forall x \in \mathbb{R}_{+}^{\ast} \qquad 0^{x} = 0 \left(\textrm{mais } 0^{0} = 1 \right)\)
\(\forall (x,y) \in \mathbb{R}^{2} \qquad a^{x+y} = a^{x} \times a^{y}\)
\(\forall (x,y) \in \mathbb{R}^{2} \qquad a^{x-y} = \frac{a^{x}}{a^{y}}\)
\(\forall x \in \mathbb{R} \qquad a^{-x} = \frac{1}{a^{x}}\)
\(\forall (a,b) \in \left(\mathbb{R}_{+}^{\ast}\right)^{2}, \forall x \in \mathbb{R} \qquad (ab)^{x} = a^{x} b^{x}\)
\(\forall (x,y) \in \mathbb{R}^{2} \qquad \left(a^{x}\right)^{y} = a^{xy}\)
\(\forall(a,b) \in \left(\mathbb{R}_{+}^{\ast}\right)^{2}, \forall x \in \mathbb{R} \qquad \left(\frac{a}{b}\right)^{x} = \frac{a^{x}}{b^{x}}\)
Étude des fonctions \(a^{x}\) \((a \in \mathbb{R}_{+}^{\ast})\)
Les propriétés des fonctions \(a^{x}\) se déduisent de celles de \(\textrm{e}^{x}\) puisque : \(a^{x} = \exp_{a} x = \textrm{e}^{x\ln a}\).
Les fonctions \(a^{x}\) et \(\log_a x\), étant réciproques, seront représentées par des courbes symétriques par rapport à la droite d'équation \(y = x\).
Comme pour les fonctions \(\log_{a} x\) nous devons considérer les cas suivants :
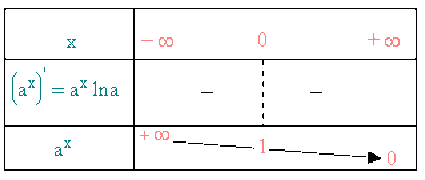
1er cas : \(0 < a < 1\) , \(\ln a < 0\) (Comportement de \(a^{x}\) contraire à celui de la fonction \(\textrm{e}^{x}\))
Domaine de définition : \(D_{f} =\mathbb{R}\)
Etude aux bornes de \(D_f\) :
Quand \(x \to - \infty \quad x\ln a \to + \infty ~\textrm{ et }~\displaystyle{\lim_{x\to -\infty} \textrm{e}^{x \ln a} \to +\infty}\)
( Branche parabolique de direction asymptotique \(y'y\) )
Quand \(x \to + \infty \quad x\ln a \to - \infty ~\textrm{ et }~\displaystyle{\lim_{x\to +\infty} \textrm{e}^{x \ln a} \to 0}\)
( Asymptote horizontale d'équation \(y = 0\) )
Fonctions dérivées
\(\left(a^{x}\right)' = \left(\textrm{e}^{x \ln a'}\right)' = a^{x} \ln a < 0\) \(a^{x}\) strictement décroissante sur \(\mathbb{R}\)
\(\left(a^{x}\right)'' = a^{x} \left(\ln a \right)^{2} >0\) \(a^{x}\) est convexe sur \(\mathbb{R}\)
Tableau de variation et graphe
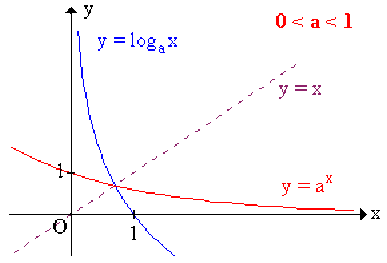
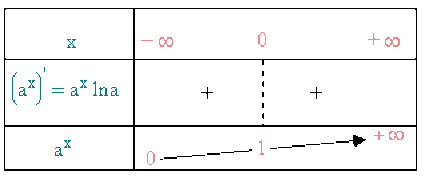
2ème cas : \(a > 1\) , \(\ln a > 0\) (Comportement de \(a^{x}\) semblable à celui de la fonction \(\textrm{e}^{x}\))
Domaine de définition : \(D_{f} = \mathbb{R}\)
Etude aux bornes de \(D_f\) :
Quand \(x \to - \infty \quad x \ln a \to -\infty \textrm{ et } \displaystyle{\lim_{x \to -\infty} \textrm{e}^{x \ln a} \to 0}\)
( Asymptote horizontale d'équation \(y = 0\) )
Quand \(x \to + \infty \quad x \ln a \to +\infty \textrm{ et } \displaystyle{\lim_{x \to +\infty} \textrm{e}^{x \ln a} \to +\infty}\)
( Branche parabolique de direction asymptotique \(y'y\) ).
Fonctions dérivées
\(\left(a^{x}\right)' = a^{x} ~\ln a > 0\) \(a^{x}\) est strictement croissante sur \(\mathbb{R}\)
\(\left(a^{x}\right)'' = a^{x} \left(\ln a \right)^{2} >0\) \(a^{x}\) est convexe sur \(\mathbb{R}\)
Tableau de variation et graphe