Différentielle d'une fonction scalaire en un point
Définition :
Si une fonction \(y = f (x)\) est dérivable en tout point d'un intervalle \(I,\) on définit la différentielle \(df\) de cette fonction par : \(\color{red}df = f '(x) \Delta x\) où \(\Delta x\) est un accroissement arbitraire de la variable \(x.\)
Dans le cas où la fonction à différencier est \(f (x) = x,\) cette relation conduit à : \(df = dx = 1 .\) \(\Delta x\) et la différentielle \(dx\) de la fonction \(x\) devient un accroissement arbitraire de la variable \(x\) d'où :
\(\boxed{\color{red}df = f '(x) dx}\)
En posant \(\Delta x = x - x_0,\) la formule de Taylor permet d'exprimer l'accroissement total \(\Delta y = f (x) - f (x_0)\) en fonction de l'accroissement de la variable \(\Delta x\) :
\(\Delta y=f(x)-f(x_0)=\frac{\Delta x}{1!}f'(x_0)+\frac{(\Delta x)^2}{2!}f''(x_0)+\ldots=df+\frac{(\Delta x)^2}{2!}f''(x_0)+\ldots\)
et
\(\Delta y-df=\frac{(\Delta x)^2}{2!}f''(x_0)+\frac{(\Delta x)^3}{3!}f'''(x_0)+\dots\)
Cette différence est d'autant plus petite que \(\Delta x\) est faible et en première approximation, on prendra : \(\color{red}\Delta y \sim dy\)
Exemple : Variation de Surface
Variation de la surface \(S = x^2\) d'un carré quand son côté augmente de \(\Delta x.\)
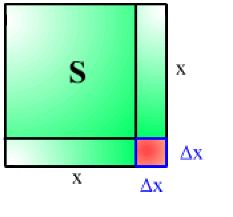
La surface du carré de côté \(x\) étant \(S = x^2,\) à l'accroissement \(\Delta x\) de la variable \(x,\) va correspondre un accroissement \(\Delta S\) de la fonction \(S,\) d'où :
\(x \rightarrow x + \Delta x~~~~ S \rightarrow S + \Delta S = (x + \Delta x)^2\)
et \(\color{red}\Delta S\color{black} = (x + \Delta x)^2 - x^2 = \color{red}2 x \Delta x + (\Delta x)^2\)
La différentielle de la surface étant \(dS = 2x \Delta x\)
nous avons \(\Delta S - dS = (\Delta x)^2\) qui tend vers \(0\) quand \(\Delta x\) tend vers \(0\)
Géométriquement cette différence représente l'aire du carré de côté \(\Delta x.\)
Opérations sur les différentielles
Cas d'une somme, d'un produit d'un quotient
En multipliant par \(dx,\) le résultat de la dérivée d'une fonction, nous obtenons sa différentielle. Donc pour deux fonctions \(u (x)\) et \(v (x),\) nous avons :
\(\begin{array}{|c|}\hline d(u+v)=du+dv\\\\d(uv)=vdu+udv\\\\d(\frac{u}{v})=\frac{vdu-udv}{v^2}\\\hline\end{array}\)
et les différentielles logarithmiques
\(\begin{array}{|c|}\hline\frac{d(uv)}{uv}=\frac{du}{u}+\frac{dv}{v}\\\\\frac{d(\frac{u}{v})}{\frac{u}{v}}=\frac{du}{u}-\frac{dv}{v}\\\hline \end{array}\)
Cas d'une fonction composée d'une variable
Connaissant la dérivée de la fonction composée \(( f [u (x]))' = f '(u) u'(x),\) nous en déduisons la différentielle :
\(\boxed{\color{red}df[(u(x))]=f'(u)u'(x)dx=f'(u)du}\)
Exemple : Différentielle d'une fonction
Soient \(u(x) = \sin x\) et \(v(x) = \cos x\) deux fonctions de la variable x. Alors :
\(d (u + v) = d(\sin x + \cos x) = d(\sin x) + d(\cos x)\)
\(= (\cos^2 x - \sin^2 x) dx\)
\(d(u v) = d(\sin x \cos x) = d(\sin x) \cos x + \sin x ~d(\cos x)\)
\(= (\cos^2x - \sin^2x) dx = \cos 2x ~dx = d( (\sin 2x) / 2)\)
\(d(\frac{u}{v})=d(\frac{\sin x}{\cos x})=\frac{\cos x~d (\sin x)-\sin x~d(\cos x)}{\cos^2x}\)
\(=\frac{\cos^2x+\sin^2x}{\cos^2x}dx=\frac{dx}{\cos^2x}\)
\(=(1+\tan^2x)dx\)
\(=d(\tan x)\)
Exemple : Différentielle d'une fonction composée
Soit \(y = \sin 5x\) alors \(y = f (u) = \sin u\) avec \(u = 5x\)
\(dy = f '(u) du = f '(u) u'(x) dx = \cos 5x . (5) dx\)
\(\color{red}dy = 5 \cos 5x dx\)
Si \(y=\exp(x^2 + 1)\) alors \(y = f (u) = e^u\) avec \(u = x^2 + 1\)
\(dy = f '(u) du = f '(u) u'(x) dx = \color{red}2x \exp(x^2 + 1) dx\)