Définition de l'intégrale définie
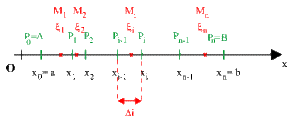
Sur un axe \(Ox\) orienté, on considère les points \(A\) et \(B\) d'abscisses respectives \(a\) et \(b\) \((b > a).\)
Positionnons entre \(A\) et \(B,\) une succession de points arbitraires \(P_i\) d'abscisses \(x_i\) pour former \(n\) intervalles de longueurs \(\Delta _i = [x_{i-1}, x_i] :\)
\(P_0 (x_0 = a),~ P_1 (x_1), ~\dots ,~ P_i (x_i),~\dots,~ P_n (x_n = b).\)
Considérons dans chaque intervalle \([x_{i-1}, x_i]\) un point \(M_i\) d'abscisse \(\zeta\)
Une fonction \(f\) définie et continue sur \([a, b]\) prendra la valeur \(f(\zeta_i)\) au point \(M_i.\)
Définition : Somme de Riemann
La somme \(S_n,\) associée à la fonction \(f\) :
\(S_n=(x_1-x_0)f(\zeta_1)+\ldots+(x_i-x_{i-1})f(\zeta_i)+\ldots+(x_n-x_{n-1})f(\zeta_n)=\sum_{i=1}^n\Delta x_if(\zeta_i)\)
avec \(\Delta x_i = x_i - x_{i-},\) \(x_0 = a\) et \(x_n = b\)
est appelée somme de Riemann de \(f\) sur \([a, b].\)
Exemple : Somme de Riemann
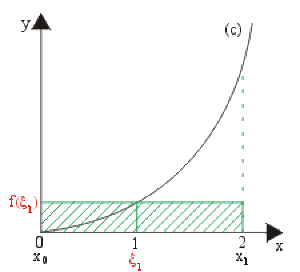
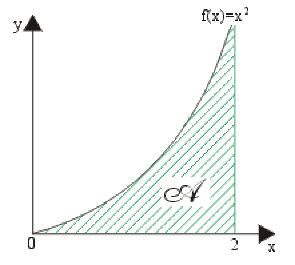
Soit la fonction \(f(x) = x^2\) définie et continue sur \([0,2].\)
Calculons la somme de Riemann dans le cas où l'intervalle \([0,2]\) est divisé en \(n = 1,\) puis \(n = 2\) intervalles avec les points \(M_i\) choisis au centre des segments \([x_{i-1}, x_i].\)
Cas où \(n = 1\) :
\(S_1=(x_1-x_0)f(\zeta_1)=2f(1)=\color{red}2~u.a.\)
\((\zeta_1=1\) et \(f(\zeta_1)=1)\)
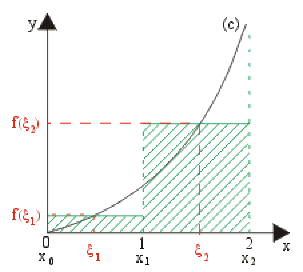
Cas où \(n = 2\) :
\(S_2=(x_1-x_0)f(\zeta_1)+(x_2-x_1)f(\zeta_2)\\=1.\frac{1}{4}+1.\frac{9}{4}=\frac{10}{4}=\frac{5}{2}=\color{red}2,5~u.a.\)
\((\zeta_1=\frac{1}{2}\) et \(f(\zeta_1)=\frac{1}{4}~~\zeta_2=\frac{3}{2}\) et \(f(\zeta_2)=\frac{9}{4})\)
Définition : Intégrale définie
On appelle intégrale définie de \(f(x)\) sur \([a, b],\) la limite, si elle existe, de la somme de Riemann \(S_n\) quand le nombre n d'intervalles tend vers l'infini (c.a.d. quand \(Dx_i \rightarrow 0)\) et sera notée :
\(\lim_{n\rightarrow+\infty }S_n=\lim_{n\rightarrow+\infty}\sum_{i=1}^n\Delta x_if(\zeta_i)=\color{red}\int_a^bf(x)dx=I\)
Cas où \(a = b\) : La somme de Riemann est nulle car \(S = (a - a) f(a) = 0\) et \(\color{red}\int_a^af(x)dx=0\)
Exemple : Somme de Riemann : Intégrale définie
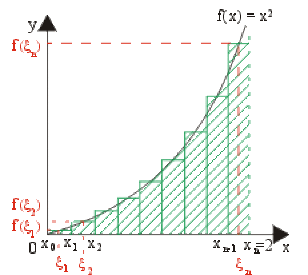
Soit la fonction \(f(x) = x^2\) définie et continue sur \([0,2].\)
La somme de Riemann \(S_n\rightarrow I=\int_0^2f(x)dx\) quand \(x\rightarrow\infty\)
Nous avons vu dans l'exercice précédent que pour \(n = 1\) et \(n = 2\) nous obtenions respectivement \(S_1 = 2~u.a.\) et \(S_2 = 2,5~ u.a.\)
Quand \(n\) croit la somme de Riemann tend vers une limite :
\(\lim_{x\rightarrow\infty}S_n\rightarrow I=\int_0^2f(x)d(x)~\#~2.67~u.a.\)
aire de la surface comprise entre la courbe \((c),\) l'axe des abscisses et les droites d'équations \(x_1 = 0\) et \(x_2 = 2.\)(voir le calcul de l'intégrale définie à partir d'une primitive de \(f(x)).\)
Cas \(n \rightarrow\infty\)
\(\lim_{n\rightarrow\infty}S_n=\lim_{n\rightarrow\infty}\sum_{i=1}^n\Delta x_if(\zeta_i)\)
\(\int_a^bf(x)dx=\mathcal A~\#~\color{red}2.7~u.a.\)
Interprétation géométrique
Soit la courbe \((C)\) représentative dans un repère orthonormé d'une fonction \(f\) définie et continue sur \([a, b].\)
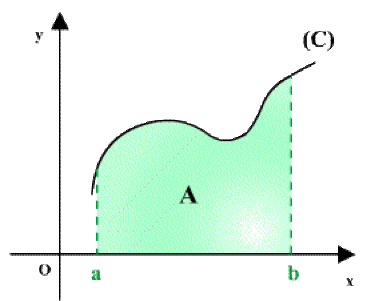
\(1^{\textrm{er}}\) cas : \(f(x)\) est positive sur \([a, b]\)
La somme de Riemann \(S_n=(x_1-x_0)f(\zeta_1)+\ldots+(x_n-x_{n-1})f(\zeta_n)=\sum_{i=1} ^n\Delta x_if(\zeta_i)\) est la somme des aires des rectangles de longueur \((x_i - x_{i-1})\) et de hauteur \(f(\zeta_i)\) (fig1). Donc \(S_n\) est une valeur approchée de l'aire du domaine \(A\) limité par la courbe \((C),\) l'axe \(Ox\) et les droites d'équation \(x = a\) et \(x = b\) (fig2). D'où :
\(\lim_{n\rightarrow+\infty}S_n=\lim_{n\rightarrow+\infty}\sum_{i=1}^n\Delta x_if(\zeta_i)\Leftrightarrow\color{red} I_1=\int_a^bf(x)dx=+A\)
fig 1
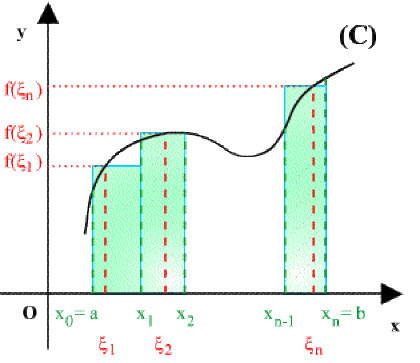
fig 2
\(2^{\textrm{ème}}\) cas : \(f(x)\) est négative sur \([a, b]\)
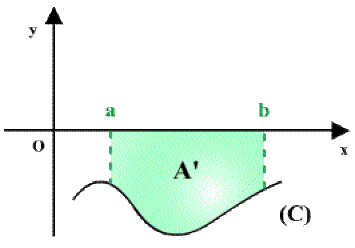
L'intégrale \(I_2=\int_a^bf(x)dx=-A'\)
(La valeur de l'intégrale est l'opposée de l'aire \(A').\)
\(3^{\textrm{ème}}\) cas : \(f(x)\) prend des valeurs positives et négatives sur \([a, b]\)
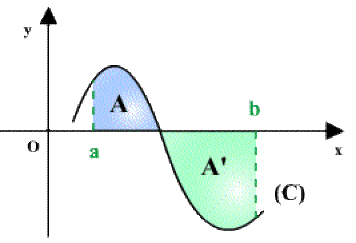
L'intégrale \(I_3=\int_a^bf(x)dx=A-A'\)
Exemple : Intégrale d'une fonction à valeurs positives
Soit la fonction \(f_1(x) = x\) définie et continue sur \([1,2].\)
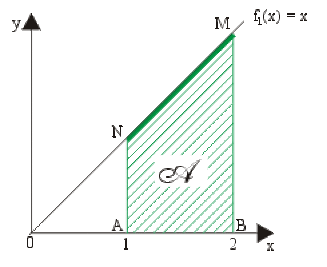
\(I_1=\int_1^2xdx=+\mathcal A=+(\textrm{aire du trapèze } ABMN)=\frac{AN+BM}{2}.AB=\color{red}\frac{3}{2}u.a.\)
Exemple : Intégrale d'une fonction à valeurs négatives
Soit la fonction \(f_2(x) = -x\) définie et continue sur \([1,3].\)
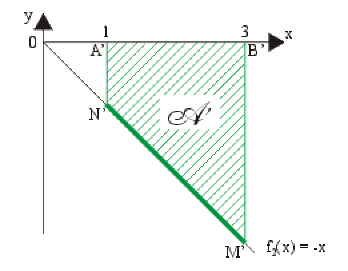
\(I_2=\int_1^3(-x)dx=-\mathcal A=-(\textrm{aire du trapèze }A'B'M'N')=-(\frac{A'N'+B'M'}{2}).A'B'=\color{red}4~u.a.\)
Exemple : Intégrale d'une fonction à valeurs positives et négatives
Soit la fonction \(f_3(x) = x\) définie et continue sur\( [-1,2].\)
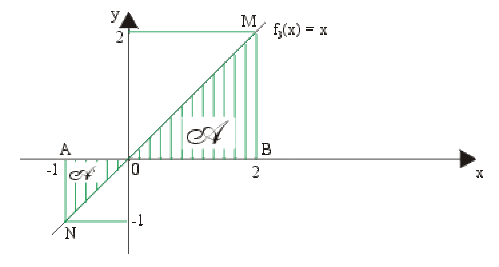
\(I_3=\int_{-1}^2xdx=\mathcal A-\mathcal A'=\textrm{aire du triangle }OBM-\textrm{aire du triangle }OAN\)
\(=\frac{MB.OB}{2}-\frac{AN.OB}{2}=2-\frac{1}{2}=\color{red}\frac{3}{2}u.a.\)
Expression de l'intégrale définie en fonction d'une des primitives F(x) de f(x)
Soient
la fonction \(y = f(x)\) représentée par la courbe \((C)\) et
une fonction primitive \(F(x)\) de \(f(x)\) représentée par l'aire \(A =( N_0M_0MN)\) avec les points d'abscisses \(N_0\) \((x_0\) fixe) et \(N\) \((x\) variable).
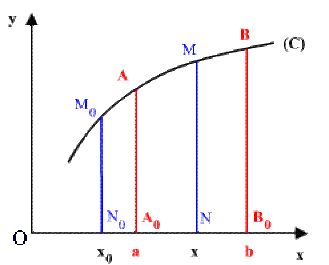
On a : \(\int_a^bf(x)dx=\textrm{aire}(A_0ABB_0)=\textrm{aire}(N_0M_0BB_0)-\textrm{aire}(N_0M_0AA_0),\)
d'où \(\boxed{\color{red}\int_a^bf(x)dx=F(b)-F(a)}\)
Exemple : Calcul d'intégrales à partir d'une primitive F(x) de f(x)
Intégrale de \(f(x) = x^2\) sur \([0,2].\)
\(I=\int_0^2x^2dx=[\frac{x^3}{3}]_0^2=\frac{8}{3}~\#~\color{red}2,67\)
\((\lim_{n\rightarrow\infty}S_n\) de la somme de Riemann)
Intégrale de \(f_1(x) = x\) sur \([1,2].\)
\(I_1=\int_1^2xdx=[\frac{x^2}{2}]^2_1=\frac{4-1}{2}=\frac{3}{2}=\color{red}1,5\)
\((+\mathcal A\):avec \(\mathcal A\) aire du trapèze \(ABMN)\)
Intégrale de \(f_2(x) = -x\) sur \([1,2].\)
\(I_2=\int_1^3(-x)dx=-[\frac{x^2}{2}]^3_1=-\frac{(9-1)}{2}=\color{red}-4\)
\((-\mathcal A'\):avec \(\mathcal A'\) aire du trapèze \(A'B'M'N')\)
Intégrale de \(f_3(x) = x\) sur \([-1,2].\)
\(I_3=\int_{-1}^2xdx=[\frac{x^2}{2}]^2_{-1}=-\frac{4-1}{2}=\frac{3}{2}=\color{red}1,5\)
\((\mathcal A-\mathcal A'\):avec \(\mathcal A\) aire du triangle \(OBM\) et \(\mathcal A'\) aire du triangle \(OAN)\)