Propriétés des intégrales définies
Soient \(f(x)\) et \(g(x)\) deux fonctions définies et continues \(\forall x \in [a, b]\) avec \(a \leq b.\)
Par application de la formule
\(\color{red}\int_a^bf(x)dx=F(b)-F(a)\)
nous avons les propriétés suivantes :
Propriété : 1 : Symétrie
\(\color{red}\int_a^bf(x)dx=-\int_b^af(x)dx\)
Démonstration :
\(\color{red}\int_a^bf(x)dx\color{black}=[F(x)]_a^b=F(b)-F(a)=-[F(a)-F(b)]=-[F(x)]_b^a = \color{red}-\int_b^af(x)dx\)
Exemple : Symétrie
\(\int_1^3x^2dx=[\frac{x^3}{3}]_1^3=\frac{27}{3}-\frac{1}{3}=\color{red}\frac{26}{3}\)
\(-\int_3^1x^2dx=-[\frac{x^3}{3}]_{3}^1=-[\frac{1}{3}-\frac{27}{3}]=\color{red}\frac{26}{3}\)
donc
\(\boxed{\int_1^3x^2dx=-\int_3^1x^2dx}\)
Propriété : 2 : Additivité
\(\color{red}\int_a^bf(x)dx=\int_a^cf(x)dx+\int_c^bf(x)dx\color{black},~~c\in[a, b]\)
(Relation de Chasles)
Démonstration :
\(\color{red}\int_a^bf(x)dx\color{black}=[F(x)]^b_a=F(b)-F(a)=F(b)-F(c)+F(c)-F(a)\\=[F(x)]]^b_c + [F(x)]^c_a=\color{red}\int_a^cf(x)dx+\int_c^bf(x)dx\)
Exemple : Additivité
Pour tout \(x \in [-2, 2],\)
\(|x| = - x\) pour \(-2 \leq x \leq 0\)
\(|x| = + x\) pour \(0 \leq x \leq 2\)
\(\int_{-2}^2|x|dx=\int_{-2}^0-xdx+\int_0^2xdx=[-\frac{x^2}{2}]_{-2}^0+[\frac{x^2}{2}]_0^2=-[0-\frac{4}{2}]+[\frac{4}{2}]=\color{red}4\)
Propriété : 3 : Multiplication par un scalaire λ
\(\color{red}\int_a^b\lambda f(x)dx=\lambda \int_a^bf(x)dx\) \(\lambda\in \mathbb R\)
Démonstration :
\(\color{red}\int_a^b\lambda f(x)dx\color{black}=[\lambda F(x)]_a^b=\lambda F(b)-\lambda F(a)\\=\lambda[F(b)-F(a)]=\lambda[F(x)]_a^b=\color{red}\lambda \int_a^bf(x)dx\)
Exemple : Multiplication par un scalaire λ
\(\int_1^33x^2dx=[x^3]_1^3=27-1=\color{red}26\)
\(3\int_1^3x^2dx=3[\frac{x^3}{3}]_1^3=3[\frac{27}{3}-\frac{1}{3}]=\color{red}26\)
donc
\(\boxed{\int_1^33x^2dx=3\int_1^3x^2dx}\)
Propriété : 4 : Distributivité par rapport à l'addition
\(\color{red}\int_a^b(\alpha f(x)+\beta g(x))dx=\alpha\int_a^b f(x)dx+\beta\int_a^bg(x)dx\)
\(\forall (\alpha, \beta)\in\mathbb R^2\)
Démonstration :
\(\color{red}\int_a^b(\alpha f(x)+\beta g(x))dx\color{black}=[\alpha F(x)+\beta G(x)]_a^b\\=(\alpha F(b)+\beta G(b))-(\alpha F(a)+\beta G(a))\\=\alpha F(b)-\alpha F(a)+\beta G(b)-\beta G(a)\\=\alpha[F(x)]_a^b-\beta[G(x)]_a^b=\color{red}\alpha\int_a^b f(x)dx+\beta\int_a^bg(x)dx\)
Exemple : Distributivité par rapport à l'addition
\(\int_0^{\pi/2}(3x+2\cos x)dx=[3\frac{x^2}{2}+2\sin x]_0^{\pi/2}=\color{red}\frac{3\pi^2}{8}+2\)
\(3\int_0^{\pi/2} xdx+2\int_0^{\pi/2} \cos xdx=3[\frac{x^2}{2}]_0^{\pi/2}+2[\sin x]_0^{\pi/2}=\color{red}\frac{3\pi^2}{8}+2\)
donc
\(\boxed{\int_0^{\pi/2}(3x+2\cos x)dx=3\int_0^{\pi/2}xdx+2\int_0^{\pi/2}\cos xdx}\)
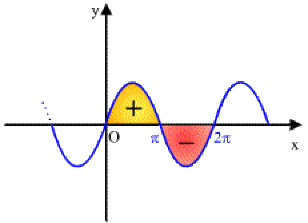
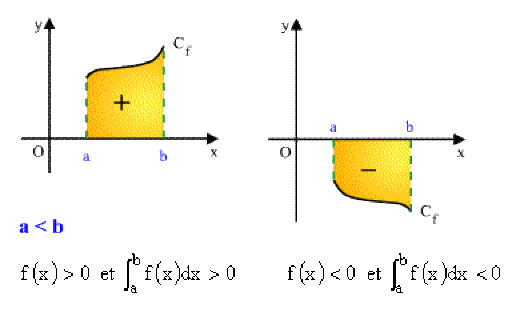
Propriété : 5 : Signe de l'intégrale
Si \(f \geq 0\) (resp. \(\leq 0)\) alors \(\color{red}\int_a^bf(x)dx\geq0\) (resp.\(\leq 0)\)
Exemple : Signe de l'intégrale (1)
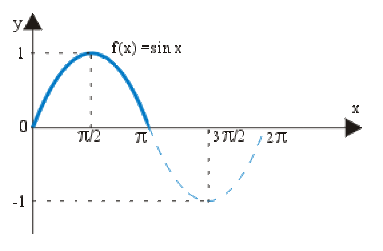
Exemple : Signe de l'intégrale (2)
\(\sin x \geq 0\) pour \(x\in[0,\pi]\)
\(\int_0^{\pi}\sin xdx=[-\cos x]_0^{\pi}=2 > 0\)
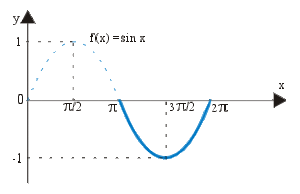
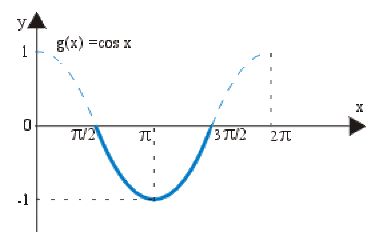
\(\cos x \leq 0\) pour \(x\in[\pi/2, 3\pi/2]\)
\(\int_{\pi/2}^{3\pi/2}\cos xdx=[\sin x]_{\pi/2}^{3\pi/2}=-2 <0\)
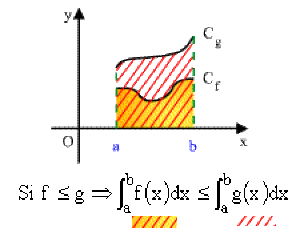
Propriété : 6 : Comparaison d'intégrale
Si \(f \leq g\) alors \(\color{red}\int_a^bf(x)dx\leq\int_a^bg(x)dx\)
Exemple : Comparaison d'intégrale
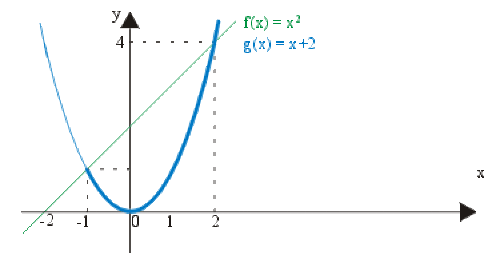
Pour \(x\in[-1,2]~~f(x)\leq g(x)\)
et \(\int_{-1}^2f(x)dx=\int_{-1}^2x^2dx=[\frac{x^3}{3}]_{-1}^2=3\)
\(\int_{-1}^2g(x)dx=\int_{-1}^2(x+2)dx=[\frac{x^2}{2}+2x]_{-1}^2=\frac{15}{2}\)
d'où \(\color{red}\boxed{\color{black}f(x) \leq g(x)\rightarrow\int_{-1}^2f(x)dx\leq\int_{-1}^2g(x)dx}\)
Propriété : 7 : Inégalité de la moyenne
Si \(m \leq f(x) \leq M\) alors
\(\color{red}m(b-a)\leq\int_a^bf(x)dx\leq M(b-a)\)
\((m,M)\in\mathbb R^2\)
Exemple : Inégalité de la moyenne
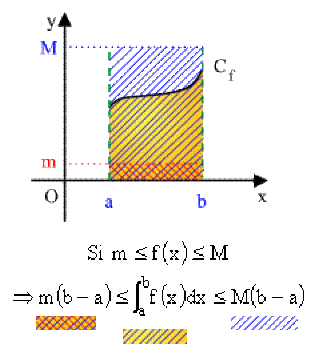
\(f(x)=\sin x\) pour \(x\in[0,3\pi/2]\)
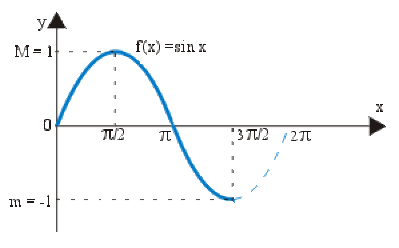
Nous avons : \(-1\leq \sin x\leq 1,\) puis successivement \(m(b-a)=-1(3\pi/2-0)=-3\pi/2\)
\(\int_0^{3\pi/2}\sin xdx=[-\cos x]_0^{3\pi/2}=1\)
\(M(b-a)=1(3\pi/2-0)=3\pi/2\)
D'où \(\color{red}\boxed{\color{black}-3\pi/2\leq\int_0^{3\pi/2}\sin xdx=1=3\pi/2}\)
Propriété : 8 : Majoration de la valeur absolue d'une intégrale
Si \(| f | \leq M,\) sur \([a, b]\) alors :
\(\color{red}|\int_a^bf(x)dx|\leq\int_a^b|f(x)|dx\leq M(b-a)\)
Exemple : Majoration de la valeur absolue d'une intégrale
Si \(|f|\leq M\) avec \(a\leq b\) alors
\(|\int_a^bf(x)dx|\leq\int_a^b|f(x)|dx\leq M(b-a)\)
Puisque \(|\sin x|\leq 1\) pour \(x\in[\pi,2\pi]\) nous avons :
\(|\int_{\pi}^{2\pi}\sin xdx|=|[-\cos x]_{\pi}^{2\pi}|=|-\cos2\pi+\cos\pi|=|-2|=2\)
\(M(b-a)=1(2\pi-\pi)=\pi\)
D'où \(\color{red}\boxed{\color{black}|\int_{\pi}^{2\pi}\sin x dx|=2\leq \pi}\)
Propriété : 9 : Propriétés des fonctions paires, impaires et périodiques
Si \(f\) est paire, \(f(-x) = f(x),\) alors
\(\color{red}\int_{-a}^af(x)dx=2\int_0^af(x)dx\)
Si \(f\) est impaire, \(f(-x) = - f(x),\) alors
\(\color{red}\int_{-a}^af(x)dx=0\)
Si \(f\) est périodique, de période \(T,\) \(f(x + T) = f(x),\) alors
\(\color{red}\int_a^{a+T}f(x)dx=\int_0^Tf(x)dx\)
Exemple : Propriétés des fonctions paires
Fonction paire : \(\int_{-a}^af(x)dx=2\int_0^af(x)dx\)
ici \(\color{blue}f(x)=x^2\)
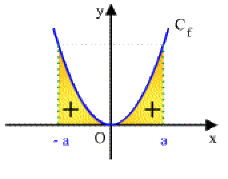
Exemple : \(\int_{-2}^2x^2dx=[\frac{x^3}{3}]_{-2}^2=\frac{8}{3}-(-\frac{8}{3})=2\times\frac{8}{3}=2\int_0^2x^2dx\)
Exemple : Propriétés des fonctions impaires
Fonction impaire : \(\int_{-a}^af(x)dx=0\)
ici \(\color{blue}f(x)=x^3\)
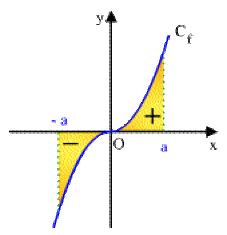
Exemple : \(\int_{-1}^1x^3dx=[\frac{x^4}{4}]_{-1}^1=\frac{1}{4}-\frac{1}{4}=0\)
Exemple : Propriétés des fonctions périodiques
Fonction \(f\) périodique de période \(T\) :
\(\int_a^{a+T}f(x)dx=\int_0^Tf(x)dx\)
ici \(\color{blue}f(x)=\sin x\)
\(\int_{\pi/2}^{\pi/2+2\pi}\sin xdx=[-\cos x]_{\pi/2}^{5\pi/2}=-\cos\frac{5\pi}{2}+\cos\frac{\pi}{2}=0+0=0\)
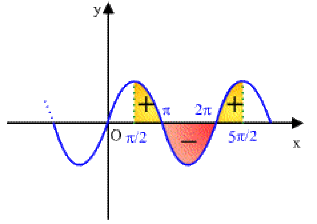
\(\int_0^{2\pi}\sin xdx=[-\cos x]_0^{2\pi}=-\cos2\pi+\cos 0=-1+1=0\)
