Le pendule simple
Partie
Question
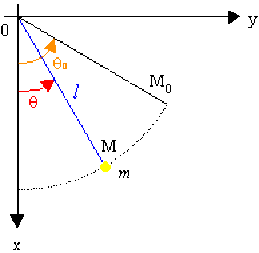
Un pendule simple est constitué d'un objet ponctuel \(M\) de masse \(m\), suspendu à un fil inextensible de longueur \(l\). On le lâche, sans vitesse initiale de la position \(\theta_{0}\).
L'oscillation s'effectue dans le plan \(xOy\); la position du mobile, à l'instant \(t\), est repérée par l'angle \(\theta = \Big( \overset{\rightarrow}{Ox}, \overset{\longrightarrow}{OM} \Big)\).
On néglige tous les frottements.
Par application du Principe Fondamental de la Dynamique, déterminer l'équation différentielle du mouvement dans le cas des petites oscillations.
Aide simple
Appliquer à la masse \(m\) le Principe Fondamental de la Dynamique sous forme vectorielle.
Aide détaillée
Se donner un repère (par exemple \(\overset{\rightarrow}{u_{r}}\) et \(\overset{\rightarrow}{u_{\theta}}\)) lié à la masse \(m\) sur lequel l'égalité vectorielle \(m\overset{\rightarrow}{\gamma} = \underset{i}{\sum} \overset{\longrightarrow}{F_{i}}\).
Le vecteur accélération \(\overset{\rightarrow}{\gamma}\) sera calculé dans \((\overset{\rightarrow}{u_{r}}, \overset{\rightarrow}{u_{\theta}})\) par l'intermédiaire des vecteurs \(\overset{\longrightarrow}{OM}\) et \(\frac{\textrm{d} \overset{\longrightarrow}{OM}}{\textrm{d}t}\).
Solution simple
Principe Fondamental de la Dynamique : \(m \overset{\rightarrow}{\gamma} = \overset{\rightarrow}{P} + \overset{\rightarrow}{T}\)
La projection de cette égalité sur \(\overset{\rightarrow}{u}_{\theta}\), conduit pour les petites oscillations à : \(\ddot{\theta} + \frac{g}{l}~\theta = 0\)
Solution détaillée
Principe Fondamental de la Dynamique : \(m \overset{\rightarrow}{\gamma} = \underset{i}{\sum} \overset{\rightarrow}{F_ {i}} = \overset{\rightarrow}{P} + \overset{\rightarrow}{F}\)
En projetant cette égalité sur le repère \((\overset{\rightarrow}{u_{r}}, \overset{\rightarrow}{u_{\theta}})\) :
sur \(\overset{\rightarrow}{u_{r}} \qquad m \gamma_{r} = mg \cos{\theta} -T \quad \color{blue}(1)\)
sur \(\overset{\rightarrow}{u_{\theta}} \qquad m \gamma_{\theta} = -mg \sin{\theta} \quad \color{blue}(1)\)
Les expressions \(\gamma_{r}\) et \(g_{q}\) s'expriment à partir de \(\overset{\longrightarrow}{OM} = l~\overset{\rightarrow}{u_{r}}\), d'où :
\(\frac{\textrm{d} \overset{\rightarrow}{OM}}{\textrm{d}t} = l \frac{\textrm{d}\overset{\rightarrow}{u_{r}}}{\textrm{d} t} = l \frac{\textrm{d}\overset{\rightarrow}{u_{r}}}{\textrm{d} \theta}~.~\frac{\textrm{d} \theta}{\textrm{d}t} = l~\dot{\theta}~\overset{\rightarrow}{u_{\theta}}\)
\(\frac{\textrm{d}^{2} \overset{\rightarrow}{OM}}{\textrm{d}t^{2}} = l~\ddot{\theta}~\overset{\rightarrow}{u_{\theta}} + l~\dot{\theta}~\frac{\textrm{d}\overset{\rightarrow}{u_{\theta}}}{\textrm{d}\theta}~.~\frac{\textrm{d}\theta}{\textrm{d}t} = l \ddot{\theta}~\overset{\rightarrow}{u_{\theta}} - l \dot{\theta}^{2} \overset{\rightarrow}{u_{r}} = \gamma_{\theta}~\overset{\rightarrow}{u_{\theta}}+\gamma_{r}~\overset{\rightarrow}{u_{r}}\)
L'équation \(\textcolor{blue}{(2)}\) conduit, dans le cas des petites oscillations, \(\sin{\theta} \approx \theta\), à l'équation différentielle : \(ml~\ddot{\theta} = - mg \sin{\theta} \approx - mg \theta\)
\(\textcolor{red}{\ddot{\theta} + \frac{g}{l}~\theta = 0}\)
Question
Déterminer la solution générale \(\theta (t)\) par intégration d'une équation différentielle du type ( ? ).
Aide simple
Multiplier les deux membres de cette équation par \(2 (\textrm{d}q / \textrm{d}t)~\textrm{d}t\).
Aide détaillée
Obtenir une équation à variables séparables de la forme : \(f(\theta)~\textrm{d}\theta = \textrm{d}t\).
Solution simple
Après multiplication par \(2 (\textrm{d}q / \textrm{d}t)~\textrm{d}t\) nous obtenons \(\color{red} \frac{\textrm{d}\theta}{\textrm{d}t} = \pm \sqrt{K_{1} - \frac{g}{l}~\theta^{2}}\) avec \(K_{1}\) constante.
Après intégration de l'Equation à variables séparables : \(\color{red}\theta = K \sin \left( \sqrt{\frac{g}{l}} t + \rho \right)\) (\(K\) et \(\rho\) constantes).
Période des oscillations : \(\color{red} T_{0} = 2 \pi \sqrt{\frac{l}{g}}\).
Solution détaillée
Pour résoudre l'équation différentielle : \(\frac{\textrm{d}^{2} \theta}{\textrm{d}t^{2}} = - \frac{g}{l} \theta\)
multiplions les deux membres par \(2 (\textrm{d}q / \textrm{d}t)~\textrm{d}t\) :
\(2 \frac{\textrm{d} \theta}{\textrm{d}t} \frac{\textrm{d}^{2} \theta}{\textrm{d}t^{2}} \textrm{d}t = -2~\frac{g}{l}~\theta~\textrm{d}\theta\)
\(d \left[ \left( \frac{\textrm{d} \theta}{\textrm{d}t} \right)^{2} \right] = -2~\frac{g}{l}\theta~\textrm{d}\theta\)
intégrons :
\(\left( \frac{\textrm{d}\theta}{\textrm{d}t} \right)^{2} = - \frac{g}{l} \theta^{2} + K_{1}^{2}\) où \(K_{1}\) est constante
\(\frac{\textrm{d}\theta}{\textrm{d}t} = \pm \sqrt{K_{1} - \frac{g}{l} \theta^{2}}\)
séparons les variables :
\(\pm \frac{\textrm{d}\theta}{\sqrt{K_{1} - \frac{g}{l} \theta^{2}}} = \textrm{d}t\)
puis intégrons de nouveau en remarquant la forme du membre de gauche : \(\textrm{d}u / (1 - u^{2})^{1/2}\)
\(\pm \displaystyle{ \int{ \frac{\textrm{d} \theta}{\sqrt{K_{1}} \sqrt{1 - \left( \sqrt{\frac{g}{l K_{1}}} \theta \right)^{2}} } }} = \int \textrm{d}t\),
\(\pm \sqrt{\frac{l}{g}}~\textrm{Arc} \sin \sqrt{\frac{g}{l K_{1}}} \theta = t + \mathcal{C}\) où \(\mathcal{C}\) est une constante,
\(\pm \textrm{Arc}~\sin{\sqrt{\frac{g}{l K_{1}}}} \theta = \sqrt{\frac{g}{l}}t + \rho\) avec \(\rho = \sqrt{\frac{g}{l}} \mathcal{C}\),
Ainsi, \(\color{red} \theta = K \sin \left( \sqrt{ \frac{g}{l}}~t + \rho \right)\) où \(\color{red} K = \pm~( l K_{1} / g)^{1/2}\)
Par définition, la pulsation \(\omega_{0} = (g / l)^{1/2}\) permet de définir la période \(T_{0}\) des oscillations \(\omega_{0} = 2\pi / T_{0}\),
donc : \(\color{red} T_{0} = 2 \pi \sqrt{\frac{l}{g}}\)
Question
Trouver la solution particulière, vérifiant les conditions initiales.
Aide simple
La détermination des constantes nécessitent deux conditions initiales.
Aide détaillée
Première condition : \(\theta(0) = \theta_{0}\)
Deuxième condition : \(\dot{\theta}(0) = 0\)
Solution simple
Résultats :
\(\color{red} K = \theta_{0}\)
et
\(\color{red} \rho = \pi / 2\)
Solution détaillée
Les constantes d'intégration \(K\) et \(\rho\) sont déterminées par deux conditions initiales :
\(\theta(0) = \theta_{0} \Rightarrow \color{blue} \theta_{0} = K \sin{\rho} \qquad (1)\)
\(\dot{\theta}(0) = 0 \Rightarrow \color{blue} 0 = K \sqrt{\frac{g}{l}} \cos{\rho} \qquad (2)\)
La condition \(\color{blue}(2)\) détermine \(\rho = \pi / 2 (\textbf{mod}~\pi)\) qui porté dans \(\color{blue}(1)\) : \(K = \theta_{0}\),
d'où : \(\color{red} \theta = \theta_{0} \sin\left( \sqrt{\frac{g}{l}} t + \frac{\pi}{2} \right) = \theta_{0} \cos \omega_{0} t\) avec \(\color{red} \omega_{0} = \sqrt{\frac{g}{l}}\)