Somme de deux tensions
Durée : 5 mn
Note maximale : 5
Question
Déterminer à partir de la méthode de Fresnel la somme \(u(t)=u_1(t)+u_2(t)\) avec
\(\displaystyle{ u_1(t) = 4 \sqrt{2} . \cos \left( 3t + \frac{\pi}{4} \right) }\) et \(u_2(t)=3 . \cos (3t)\)
Solution
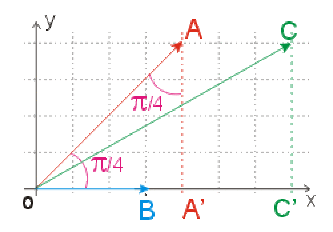
On pose : \(\overrightarrow{OA} = \vec v_1\) ; \(\overrightarrow{OB} = \vec v_2\) ; \(\overrightarrow{OC} = \vec v = \vec v_1 + \vec v_2\)
Pour trouver la norme de \(\vec v\) on utilise la relation dans le triangle \(OAC\) :
\(OC^2 = OA^2+AC^2-2 . OA . AC . \cos \hat{A} = 65\) ; donc \(OC \approx \mathrm{8,06}\).
L'angle \(\varphi\) que fait \(OC\) avec l'axe \(Ox\) est obtenu dans le triangle \(OC'C\) : \(\displaystyle{ \sin \varphi = \frac{CC'}{OC} }\) et \(\displaystyle{ CC' = AA' = OA . \sin \left(\frac{\pi}{4} \right) }\) ;
\(\varphi = \mathrm{0,52 rad} \approx 30°\)
\(u(t) = OC . \cos (3t + \varphi)\)
Barème :
Construction de \(\vec v_1\) et \(\vec v_2\) : 1 pt
Construction de \(\vec v_1 + \vec v_2\) : 1 pt
Calcul de \(u_m = OC\) : 1 pt
Calcul de \(\varphi\) : 1 pt
Expression de \(u(t)\) : 1 pt