Oscillateur harmonique forcé, oscillations forcées

Dans le cas d'une excitation sinusoïdale de pulsation \(\Omega\) variable et dans le cas où \(\lambda < \omega_0 / \sqrt{2}\), on définit la bande passante en pulsation de l'oscillateur par l'intervalle :

\(\Delta \Omega = \Omega_2 - \Omega_1 ~~~~(\Omega_2 > \Omega_1)\)

où les pulsations \(\Omega_1\) et  \(\Omega_2\) correspondent aux amplitudes \(x_{pm}(\Omega_1)\) et \(x_{pm}(\Omega_2)\) telles que :

\(x_{pm} ( \Omega_1) = x_{pm}(\Omega_2) = \frac{x_{pm}~(\Omega_r)}{\sqrt{2}}\) (figure ci-dessous)

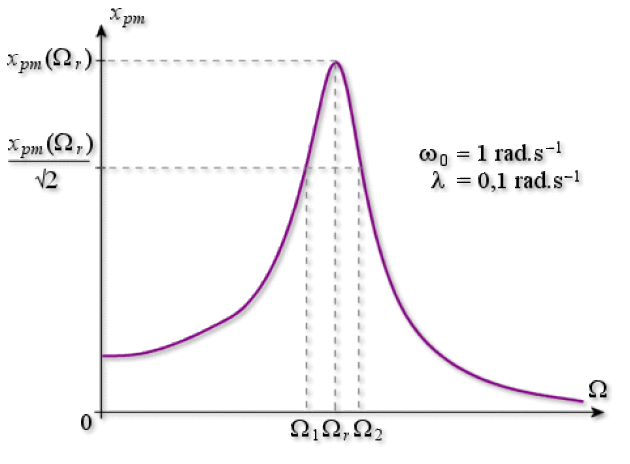
L'acuité de la résonance est définie par : \(A_c = \frac{\Omega_r}{ \Delta \Omega}\).

Ces quantités sont définies également en fréquence respectivement par \(\Delta f = f_2 - f_1\) et \(A_c = \frac{f_r}{\Delta f} = \frac{\Omega_r}{\Delta \Omega} \).

Par définition les valeurs des pulsations, \(\Omega_1\) et \(\Omega_2\) définissant la bande passante, vérifient l'équation :

\(\frac{F_m / m}{\sqrt{(\omega_0^2 -  \Omega_{1,2}^2)^2 + (2 \lambda \Omega_{1,2})^2}} = \frac{1}{\sqrt{2}} \frac{F_m / m}{2 \lambda\sqrt{\omega_0^2 - \lambda^2}}\)

La courbe de résonance en amplitude présente, dans le cas de l'amortissement très faible, un pic très marqué. Les valeurs de \(\Omega_1\) et de \(\Omega_2\) étant très proches de celles de \(\Omega_r\), on pose :

\(\Omega_{1,2}^2 = \Omega_r^2 + \varepsilon~~~~\) (\(\varepsilon\) étant un terme petit, positif ou négatif)

En remplaçant \(\Omega_r\) par l'expression de sa définition il vient : \(\Omega_{1,2}^2 = \omega_0^2 - 2 \lambda^2 + \varepsilon\) .

Reportons cette valeur dans l'équation (1) précédente. On obtient la nouvelle équation :

\(\varepsilon = \pm 2 ~\lambda \sqrt{\omega_0^2 - \lambda^2}\)

On en déduit : \(\varepsilon = \pm 2 ~\lambda ~\omega_0\sqrt{1 - \frac{\lambda^2}{\omega_0^2}} \approx \pm2  \lambda \omega_0\) (amortissement très faible, \(\lambda \ll \omega_0\))

Et également : \(\varepsilon \approx \pm 2 ~\lambda ~ \Omega_r\) (amortissement faible, \(\Omega_r \approx \omega_0\)),

D'autre part : \(\Omega_{1,2} = \sqrt{\Omega_r^2 + \varepsilon} = \Omega_r \sqrt{1 + \frac{\varepsilon}{\Omega_r^2}}\approx \Omega_r(1 + \frac{\varepsilon}{2 \Omega_r^2}) = \Omega_r + \frac{\varepsilon}{2 \Omega_r}\), \(\varepsilon\) étant petit.

Introduisons la dernière expression de \(\varepsilon\), il vient : \(\Omega_{1,2} \approx \Omega_r \pm \frac{2~ \lambda~ \Omega_r}{2~ \Omega_r} = \Omega_r \pm \lambda\), et par suite :

\(\Omega_1 \approx \Omega_r - \lambda~~\) et \(~~\Omega_2 \approx \Omega_r + \lambda\).

La bande passante, dans le cas de l'amortissement très faible, s'écrit :

\(\Delta \Omega = \Omega_2 - \Omega_1 \approx 2 \lambda = \frac{\omega_0}{Q}\)

On constate que plus le facteur de qualité \(Q\) de l'oscillateur est grand plus la bande passante est étroite.

Rappelons que plus \(Q\) est grand, plus l'amplitude des oscillations à la résonance est grande.

Enfin, l'acuité de la résonance d'un oscillateur très faiblement amorti est égale au facteur de qualité :

\(A_c = \frac{\Omega_r}{\Delta \Omega} \approx \frac{\omega_0}{\Delta\Omega} = Q\)