Circuit à trois branches
Durée : 15 mn
Note maximale : 9
Question
On considère le circuit ci-dessous :
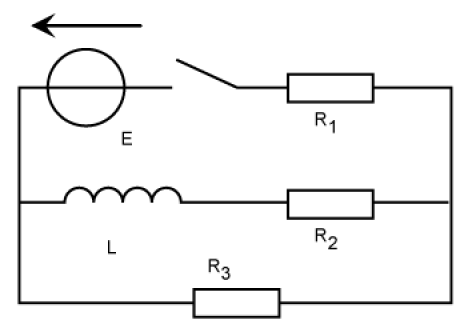
On ferme l'interrupteur à \(t = 0\) ; déterminer les équations d'évolution des courants dans toutes les branches.
Application numérique :
\(R_1 = R_2 = R_3 = R = 30 \mathrm{ } \Omega\) ;
\(L = 500 \mathrm{ mH}\) ;
\(E = 6 \mathrm{ V}\).
Solution
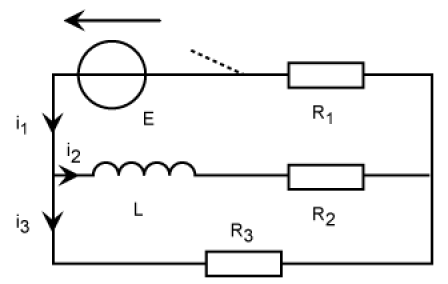
Avant la fermeture de l'interrupteur, l'intensité est nulle dans les 3 branches.
Quand l'interrupteur est fermé, la tension est la même aux bornes des 3 branches ; si les branches sont affectées de l'indice de la résistance qu'elles contiennent :
\(\displaystyle{ E - R_1 . i_1(t) = L . \frac{\mathrm{d} i_2}{\mathrm{d} t} + R_2 . i_2(t) = R_3 . i_3(t) }\)
La loi aux nœuds donne : \(i_1 = i_2 + i_3\)
Les deux premiers termes de l'équation donnent :
\(\displaystyle{ i_1(t) = \frac{E - L . \frac{\mathrm{d} i_2}{\mathrm{d} t} - R_2 . i_2}{R_1} = \frac{E}{R} - \frac{L}{R} . \frac{\mathrm{d} i_2}{\mathrm{d} t} - i_2 }\)
Les deux derniers termes de l'équation donnent :
\(\displaystyle{ i_3(t) = \frac{L . \frac{\mathrm{d} i_2}{\mathrm{d} t} + R_2 . i_2}{R_3} = \frac{L}{R} . \frac{\mathrm{d} i_2}{\mathrm{d} t} + i_2 }\)
Relations qui, reportées dans l'équation aux noeuds, conduisent à :
\(\displaystyle{ i_2 . \frac{R_1 . R_3 + R_2 . (R_1 + R_3)}{R_1 . R_3} + L . \frac{\mathrm{d} i_2}{\mathrm{d} t} . \frac{R_1 + R_3}{R_1 . R_3} = \frac{E}{R_1} }\)
\(\Rightarrow\) \(\displaystyle{ 3 . i_2 + \frac{2 . L}{R} . \frac{\mathrm{d} i_2}{\mathrm{d} t} = \frac{E}{R} }\)
qui peut aussi s'écrire : \(\displaystyle{ i_2 + \frac{2 . L}{3 . R} . \frac{\mathrm{d} i_2}{\mathrm{d} t} = \frac{E}{3 . R} }\)
Il s'agit de l'équation d'un circuit du premier ordre de constante de temps : \(\displaystyle{ \tau = \frac{2 . L}{3 . R} }\) (3 pts)
La solution de cette équation est de la forme : \(\displaystyle{ i_2(t) = K . \mathrm{e}^{-{t}/{\tau}} + C}\)
où \(K\) et \(C\) sont deux constantes, la première dépendant des conditions initiales, la seconde parce que le second membre de l'équation différentielle est constant.
Détermination de la solution particulière \(C\) :
Si \(i_2(t) = C\), on a \(\displaystyle{ \frac{\mathrm{d} i_2}{\mathrm{d} t} = 0}\), et \(\displaystyle{ i_2 = \frac{E}{3 . R} = C }\)
Détermination de la constante \(K\) :
Dans une bobine, l'intensité du courant varie de façon continue ; donc, à \(t = 0\), \(i_2(0) = 0\), d'où \(K = -C\)
Finalement : \(\displaystyle{ i_2 = \frac{E}{3 . R} \left( 1 - \mathrm{e}^{-{t}/{\tau}} \right) }\)
L'intensité dans la bobine croît régulièrement de \(0\) jusqu'à la valeur finale \(\displaystyle{ C = \frac{E}{3 . R} }\) . (2 pts)
\(\displaystyle{ i_1(t) = \frac{E}{R} - \frac{L}{R} . \frac{\mathrm{d} i_2}{\mathrm{d} t} - i_2 = \frac{2 . E}{3 . R} - \frac{E}{6 . R} . \mathrm{e}^{-{t}/{\tau}} }\)
\(\displaystyle{ i_3(t) = \frac{L}{R} . \frac{\mathrm{d} i_2}{\mathrm{d} t} + i_2 = \frac{E}{3 . R} + \frac{E}{6 . R} . \mathrm{e}^{-{t}/{\tau}} }\)
Les intensités dans les autres branches décroissent de la valeur \(\displaystyle{ \frac{E}{2 . R} }\) pour \(t = 0\), à leurs valeurs en régime permanent : \(\displaystyle{ \frac{2 . E}{3 . R} }\) pour \(i_1\), \(\displaystyle{ \frac{E}{3 . R} }\) pour \(i_3\). (2 pts)
Application numérique :
\(\displaystyle{ \tau = \frac{2 . L}{3 . R} = 11 \mathrm{ ms} }\) ;
\(\displaystyle{ i_2(t) = \mathrm{6,67} . 10^{-2} . \left( 1 - \mathrm{e}^{-{t}/{\tau}} \right) }\) ;
\(\displaystyle{ i_1(t) = \mathrm{1,33} . 10^{-1} - \mathrm{1,1} . 10^{-2} . \mathrm{e}^{-{t}/{\tau}} }\) ;
\(\displaystyle{ i_3(t) = \mathrm{6,67} . 10^{-2} + \mathrm{1,1} . 10^{-2} . \mathrm{e}^{-{t}/{\tau}} }\) . (2 pts)