Réponse à une rampe
Durée : 9 mn
Note maximale : 18
Question
Un circuit série \((RL)\) est alimenté par un générateur de tension idéal dont la f.é.m. \(e(t)\) varie de manière linéaire avec le temps \(\big[e(t) = k . f\big]\) avant de se stabiliser à la valeur constante \(E\), comme l'indique la figure ci-dessous.
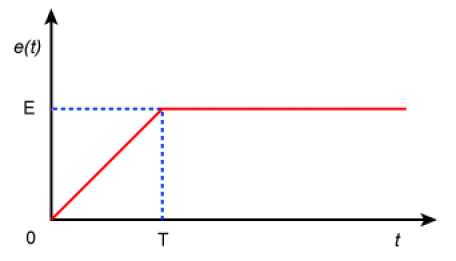
On donne \(E = 12 \mathrm{ V}\) et \(T = 2 \mathrm{ ms}\).
Déterminer, en fonction du temps, les tensions \(u_R(t)\) et \(u_L(t)\) aux bornes de \(R\) et de \(L\).
Tracer l'allure de ces deux fonctions pour \(\displaystyle{ \tau = \frac{R}{L} = \frac{T}{10} }\)
Solution
D'après la loi d'addition des tensions, \(e(t) = u_R(t) + u_L(t)\)
Comme : \(u_R(t) = R . i(t)\) et : \(\displaystyle{ u_L(t) = L . \frac{ \mathrm{d} i}{ \mathrm{d} t } =\frac{L}{R} . \frac{ \mathrm{d} u_R}{ \mathrm{d} t } }\) ,
on a la relation : \(\displaystyle{ e(t) = u_R(t) + \frac{L}{R} . \frac{ \mathrm{d} u_R}{ \mathrm{d} t } }\), qui est l'équation d'un circuit du premier ordre de constante de temps \(\displaystyle{ \tau = \frac{L}{R} }\).
La solution est donc de la forme :
\(\displaystyle{ u_R(t) = K . \mathrm{e}^{-{t}/{\tau}} + \textrm{solution particuli\`ere de l'\'equation compl\`ete} }\). (2 pts)
Recherche de la solution particulière :
De \(0\) à \(T\), la tension imposée au circuit \(RL\) suit la loi \(\displaystyle{ e(t) = E . \frac{t}{T} }\) ; nous allons donc chercher une solution particulière variant linéairement avec \(t\) : \(u_R(t) = a + b.t\), donc \(\displaystyle{ \frac{ \mathrm{d} u_R(t)}{ \mathrm{d} t } = b}\).
Remplaçons \(u_R(t)\), \(\displaystyle{ \frac{ \mathrm{d} u_R(t) }{ \mathrm{d} t } }\) et \(e(t)\) par leurs expressions dans l'équation différentielle. Il vient : \(\displaystyle{ \tau . b + a + b . t = E . \frac{t}{\tau} }\).
Pour que l'identité soit vérifiée, il faut que les termes constants et les termes du premier ordre en \(t\) aient même expression de part et d'autre du signe "égale".
D'où : \(\displaystyle{ b = \frac{E}{T} }\) et \(\displaystyle{ a = - b . \tau = -E . \frac{\tau}{t} }\).
La solution particulière est donc : \(\displaystyle{ u_R(t) = E . \frac{t - \tau}{T} }\) (3 pts)
Pour \(t > T\), la tension imposée au circuit est constante et égale à \(E\) : on cherche donc une solution particulière constante, donc \(\displaystyle{ \frac{ \mathrm{d} u_R(t) }{ \mathrm{d} t } = 0}\), ce qui donne \(u_R(t) = E\). (2 pts)
Recherche de la constante \(K\) :
La tension aux bornes d'une bobine varie de façon continue. Si, à \(t = 0\), le circuit était en régime permanent établi, à \(t = 0\) on a \(u_L(t) = 0\), donc \(u_R(t) = e(t) - u_L(t) = 0\).
\(\displaystyle{ u_R(0) = K . \mathrm{e}^{-{0}/{\tau}} + E . \frac{ 0 - \tau }{T} = 0 }\) \(\displaystyle{ \Rightarrow K = E . \frac{\tau}{T} }\)
Finalement, de \(0\) à \(T\) :
\(\displaystyle{ u_R(t) = E . \frac{\tau}{T} . \mathrm{e}^{-{t}/{\tau}} + E . \frac{ t - \tau }{T} }\)
et pour \(t = T\) : \(\displaystyle{ u_R(T) = E . \frac{\tau}{T} . \mathrm{e}^{-{T}/{\tau}} + E . \frac{ T - \tau }{T} = E - E . \frac{\tau}{T} + E . \frac{\tau}{T} . \mathrm{e}^{-{T}/{\tau}} }\)(3 pts).
Application numérique :
\(\displaystyle{ \tau = \frac{T}{10} = \mathrm{0,2 ms} }\) ;
\(\displaystyle{ u_R(t) = \mathrm{1,2} . \mathrm{e}^{-{t}/{\tau}} + 12 . \frac{t - 2 . 10^{-4}}{ 2 . 10^{-3} } }\) ;
\(\displaystyle{ u_R(T) \approx 12 - \mathrm{1,2} = \mathrm{10,8 V} }\). (3 pts)
Pour \(t \ge T\), posons \(t' = t - T\). La solution s'écrit donc : \(u_R(t') = K . \mathrm{e}^{-{t'}/{\tau}} + E\).
Pour \(t' = 0\), par continuité, \(\displaystyle{ u_R(t') = u_R(T) \approx E - E . \frac{\tau}{T} }\) (\(= \mathrm{10,8 V}\) )
\(\displaystyle{ u_R(0) = K . \mathrm{e}^{-{0}/{\tau}} + E \approx E - E . \frac{\tau}{T} }\) \(\displaystyle{ \Rightarrow K = - E . \frac{\tau}{T} }\)
Finalement :
\(\displaystyle{ u_R(t') = - E . \frac{\tau}{T} . \mathrm{e}^{-{t'}/{\tau}} + E }\) (3 pts).
Application numérique :
\(u_R(t') = - \mathrm{1,2} . \mathrm{e}^{-{t'}/{\tau}} + 12\) (2 pts)
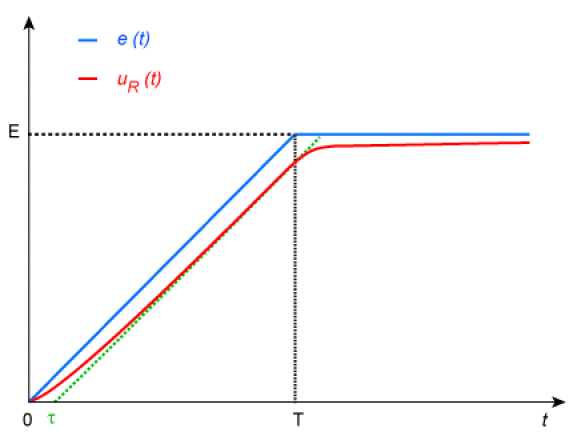
De la relation : \(e(t) = u_R(t) + u_L(t)\), on déduit : \(u_L(t) = e(t) - u_R(t)\) ; donc, de \(0\) à \(T\) :
\(\displaystyle{ u_L(T) = E . \frac{\tau}{T} - E . \frac{\tau}{T} . \mathrm{e}^{-{t}/{\tau}} - E . \frac{T - \tau}{T} = E . \frac{\tau}{T} \left( 1 - \mathrm{e}^{-{t}/{\tau}} \right) }\)
et, pour \(t > T\) :
\(\displaystyle{ u_L(t) = E . \frac{\tau}{T} . \mathrm{e}^{-{t'}/{\tau}} - E = E . \frac{\tau}{T} . \mathrm{e}^{-{t'}/{\tau}} }\) avec \(t' = t - T\), ce qui donne pour courbe :
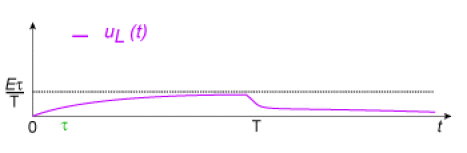
Application numérique :
\(\displaystyle{ E . \frac{\tau}{T} = \mathrm{1,2 V}}\)
de \(0\) à \(T\) :
\(\displaystyle{ u_L(t) = \mathrm{1,2} . \left( 1 - \mathrm{e}^{-{t}/{\tau}} \right) }\)
et, pour \(t > T\) ( \(t' = t - T\) ) :
\(\displaystyle{ u_L(t) = \mathrm{1,2} . \mathrm{e}^{-{t'}/{\tau}} }.\)