Réponse à une excitation harmonique
Durée : 15 mn
Note maximale : 13
Question
Soit le circuit ci-dessous,
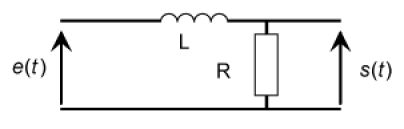
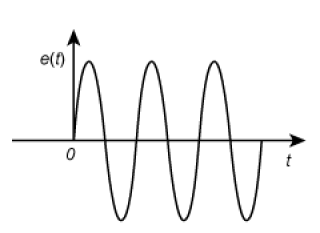
dans lequel \(e(t)\) a l'allure ci-dessous ( pour \(t < 0\) : \(e(t) = 0\) ; pour \(t \ge 0\) : \(e(t) = E_m . \sin( \omega t )\) )
Montrer que \(s(t)\) a pour équation : \(s(t) = - S_m . \sin \varphi . \mathrm{e}^{-{t}/{\tau}} + S_m . \sin (\omega t + \varphi )\)
Donner les expressions de \(S_m\) et \(\varphi\) en fonction de \(E_m\), \(R\), \(C\) et \(\omega\).
Solution
Pour \(t < 0\), \(e(t) = 0\), donc \(s(t) = 0\) en régime permanent établi.
Il a été établi précédemment que ce circuit a pour équation différentielle :
\(\displaystyle{ \tau . \frac{ \mathrm{d} s(t)}{ \mathrm{d} t } + s(t) = e(t) \mathrm{ } }\) avec pour constante de temps \(\tau = R . C\),
et que la solution est donc de la forme :
\(\displaystyle{ s(t) = K . \mathrm{e}^{-{t}/{\tau}} + \textrm{solution particuli\`ere de l'\'equation compl\`ete} }\). (3 pts)
Pour alléger le calcul, nous allons utiliser l’écriture complexe des grandeurs sinusoïdales :
\(e(t) = E_m . \sin ( \omega t ) = \mathcal{Re} \big[ \underline{e}(t) \big]\) , avec \(\displaystyle{ \underline{e}(t) = E_m . \mathrm{e}^{\mathrm{j} \omega t}}\) ;
de même la solution particulière sera cherchée en utilisant :
\(s(t) = S_m . \sin( \omega t + \varphi ) = \mathcal{Re} \big[ \underline{s}(t) \big]\) , avec \(\displaystyle{ \underline{s}(t) = S_m . \mathrm{e}^{\mathrm{j} \omega t} . \mathrm{e}^{\mathrm{j} \varphi} }\).
Avec cette écriture, \(\displaystyle{ \frac{\mathrm{d} \underline{s}(t)}{\mathrm{d} t} = \mathrm{j} . \omega . S_m . \mathrm{e}^{\mathrm{j} \omega t} . \mathrm{e}^{\mathrm{j} \varphi} }\)
et l'équation différentielle devient :
\(\displaystyle{ S_m . \mathrm{e}^{\mathrm{j} \omega t} . \mathrm{e}^{\mathrm{j} \varphi} + \mathrm{j} . \omega . \tau . S_m . \mathrm{e}^{\mathrm{j} \omega t} . \mathrm{e}^{\mathrm{j} \varphi} = E_m . \mathrm{e}^{\mathrm{j} \omega t} }\)
en simplifiant par \(\displaystyle{ \mathrm{e}^{\mathrm{j} \omega t} }\) :
\(\displaystyle{ S_m . \mathrm{e}^{\mathrm{j} \varphi} + \mathrm{j} . \omega . \tau . S_m . \mathrm{e}^{\mathrm{j} \varphi} = E_m }\)
\(\displaystyle{ S_m . ( 1 + \mathrm{j} . \omega . \tau ) . \mathrm{e}^{\mathrm{j} \varphi} = E_m}\) (4 pts)
Le second membre étant réel, l’identité n’est vraie que si le premier l’est aussi, et que leurs valeurs sont égales ;
d'où : \(\tan \varphi = - \omega . \tau = - R . C . \omega\) (condition pour que le 1er membre soit réel)
et : \(\displaystyle{ S_m = \frac{E_m}{\sqrt{1 + (R . C . \omega)^2}}}\) (condition sur les valeurs)
Finalement :
\(\displaystyle{ s(t) = K . \mathrm{e}^{-{t}/{\tau}} + S_m . \sin( \omega t + \varphi ) }\),
où \(S_m\) et \(\varphi\) ont les valeurs ci-dessus. (3 pts)
Détermination de la constante \(K\) :
En tenant compte des conditions initiales :
\(\displaystyle{ s(0) = K . \mathrm{e}^{-{0}/{\tau}} + S_m . \sin \varphi = 0}\) \(\Rightarrow K = - S_m . \sin \varphi\)
donc
\(\displaystyle{ s(t) = - S_m . \sin \varphi . \mathrm{e}^{-{t}/{\tau}} + S_m . \sin (\omega t + \varphi) }\)
CQFD
(3 pts)