Avancement de réaction [Concepts fondamentaux de la cinétique chimique]

Avancement de réaction

Définition :

Pour pouvoir étudier l'évolution de la réaction en fonction du temps et ne pas se contenter de connaître son état initial et son état final, il faut définir avec précision son avancement à tout instant. Si on a \(n_{i,0}\) moles de \(i\) à l'instant initial \(t = 0\) et \(n_i\) moles à l'instant \(t\), on définit l'avancement de la réaction à cet instant \(t\) par :

\(\mathbf{\xi=\frac{n_i-n_{i,0}}{\nu_i}}\)

\(\mathbf{\nu_i}\) est le coefficient stœchiométrique de \(i\) (affecté du signe + pour les produits et du signe – pour les réactifs).

Lorsque la substance considérée est un réactif, sa quantité diminue au cours de la réaction. Donc \(n_i - n_{i, 0}\) est négatif. Par convention on affecte le coefficient stœchiométrique \(\nu_i\) du signe moins ; il en résulte que l'avancement de la réaction \(\xi\) est positif.
Lorsque la substance considérée est un produit (\(n_i > n_{i, 0}\)), sa quantité augmente au cours de la réaction. Donc \(n_i - n_{i, 0}\) est positif. Le coefficient stœchiométrique \(\nu_i\) étant affecté du signe plus ; il en résulte que l'avancement de la réaction \(\xi\) est positif.

Remarque :

Comme son nom l'indique, la valeur de l'avancement de la réaction augmente \(\mathbf\xi\) lorsque la réaction avance.
La dimension de \(\mathbf\xi\) est celle d'une quantité de matière, c'est donc une grandeur extensive. L'unité dans le système international est la mole.
La valeur de l'avancement de la réaction \(\mathbf\xi\) ne dépend pas du choix de la substance (réactif ou produit) utilisée pour le calculer (c'est d'ailleurs son principal intérêt).
En pratique, pour le calcul de l'avancement de la réaction, on utilise la substance qui est la plus facile à doser. Mais ATTENTION, ceci n'est vrai que si la réaction est la seule qui fasse intervenir les réactifs et produits considérés (on dit que la réaction est isolée) et qu'il n'y ait pas de produits intermédiaires formés.
Le fait que l'avancement soit une grandeur extensive a pour conséquence que, pour une même quantité de matière transformée, la valeur de \(\xi\) dépend des coefficients stœchiométriques, donc de la manière d'écrire l'équation chimique.

Note : cette notion d'avancement de la réaction est développée dans le module : "Thermodynamique de la transformation Chimique".

Exemple : La valeur de l'avancement de la réaction ne dépend pas du choix de la substance (réactif ou produit) utilisée pour la calculer

Considérons la réaction de combustion de l'éthane :

\(\mathbf{\textrm C_2\textrm H_6 + \frac{7}{2}. \textrm O_2 = 2. \textrm{CO}_2 + 3. \textrm H_2\textrm O}\)

Soient au départ 3 moles d'éthane dans un excès de dioxygène.

Calculons l'avancement \(\xi\) de la réaction lorsque 2 moles d'éthane ont réagi. Faisons d'abord le calcul pour l'éthane. Lorsque 2 moles d'éthane ont été consommées, il reste 1 mole d'éthane.

D'où : \(\mathbf{\xi=\frac{n_i-n_{i,0}}{\nu_i}=\frac{1-3}{-1}=2 \textrm{moles}}\)

Faisons maintenant le calcul pour le dioxygène. La quantité de dioxygène consommée est égale à la quantité d'éthane (2 moles) ayant réagit multiplié par \(\frac{7}{2}\) soit : \(2\times\frac{7}{2} = 7\textrm{ moles}\).

D'où : \(\mathbf{\xi=\frac{n_i-n_{i,0}}{\nu_i}=\frac{-7}{-7/2}=2 \textrm{moles}}\)

On trouve donc bien la même valeur de l'avancement de la réaction quelle que soit la substance choisie pour le calculer.

On trouverait le même résultat en faisant le calcul avec les produits.

Calcul avec \(\textrm{CO}_2\) :

La quantité de \(\textrm{CO}_2\) formée est égale au double de la quantité d'éthane disparue soit \(2 \times 2 = 4\textrm{ moles}\).

D'ou \(\xi=\frac{n_i-n_{i,0}}{\nu_i}=\frac{4}{2}=2 \textrm{moles}\)

Calcul avec \(\textrm H_2\textrm O\) :

La quantité de \(\textrm H_2\textrm O\) formée est le triple de la quantité d'éthane disparue soit \(3 \times 2 = 6\textrm{ moles}\).

D'ou \(\xi=\frac{n_i-n_{i,0}}{\nu_i}=\frac{6}{3}=2 \textrm{moles}\)

Exemple : Lorsqu'une substance (réactif ou produit) intervient dans plusieurs réactions, la valeur de l'avancement dépend du choix de la substance utilisée pour la calculer.

Lorsqu'une réaction est isolée, la valeur de l'avancement de la réaction ne dépend pas du choix de la substance (réactif ou produit) utilisée pour le calculer. Ceci n'est plus vrai lorsqu'un même réactif (ou produit) intervient dans plusieurs réactions ayant lieu simultanément. Par exemple, considérons le cas de la combustion d'un mélange de méthane et d'éthane. Les deux réactions ont lieu simultanément et peuvent s'écrire :

\(\mathbf{(1) \textrm{CH}_4 + 2. \textrm O_2 = \textrm{CO}_2 + 2. \textrm H_2\textrm O}\)

\(\mathbf{(2) \textrm C_2\textrm H_6 + \frac{7}{2}. \textrm O_2 = 2. \textrm{CO}_2 + 3. \textrm H_2\textrm O}\)

Pour calculer l'avancement des deux réactions, il faut connaître les quantités transformées des réactifs et/ou des produits. Soit par exemple, un mélange de 0,5 moles de méthane \(\textrm{CH}_4\) et d'une mole d'éthane \(\textrm C_2\textrm H_6\) qui réagissent complètement dans un excès d'oxygène. Les quantités transformées sont :

	CH₄	C₂H₆	O₂	CO₂	H₂O
n_i - n_{i, 0}	- 0,5	- 1,0	- 4,5	2,5	4,0

Essayez de retrouver ces résultats intermédiaires par vous-même.

Si vous savez retrouver ces valeurs, passez au calcul de l'avancement des réactions.

Si vous ne parvenez pas à retrouver ces valeurs, procédez en plusieurs étapes, en essayant de remplir le tableau ci-dessous. En effet, pour calculer les quantités transformées, il est utile de remplir un tableau avec les quantités initiales (\(n_{i,0}\) ), restantes (\(n_i\) ) et (\(n_i - n_{i,0}\) ) transformées de chaque substance :

	CH₄	C₂H₆	O₂	CO₂	H₂O
n_i,0
n_i
n_i - n_i,0

Cliquez ici pour voir les résultats^[1] de ce tableau et les explications associées aux valeurs trouvées.

Cliquez sur avancement^[2] pour obtenir le détail du mode de calcul de l'avancement des réactions... mais prenez le temps d'essayer de trouver ces résultats...

On remarque que certains réactifs ne participent qu'à une seule des deux réactions.

C'est le cas du méthane \(\textrm{CH}_4\) pour la première réaction et de l'éthane \(\textrm C_2\textrm H_6\) pour la seconde. Il est donc possible de calculer séparément l'avancement de chaque réaction en se basant uniquement sur les quantités transformées de ces réactifs.

Pour la réaction (1), on obtient : \(\xi_1 = \textrm{0,5}\)

Pour la réaction (2), on obtient : \(\xi_2 = \textrm{1,0}\)

Pour les composé qui participent aux deux réactions, il est facile relier leur quantité transformée aux avancements des deux réactions :

\(\mathbf{n_i-n_{i,0}=\nu_{i1}.\xi_1+\nu_{i2}.\xi_2}\)

Appliquons cette relation aux autres constituants du système, on retrouve évidemment les valeurs précédemment calculées.

\(\displaystyle{\begin{array}{ccccc} \textrm{Pour le dioxygène} & \mathbf{n_i-n_{i,0}}=(-2)\times\textrm{0,5}+(-\frac{7}{2})\times\textrm{1,0} =-\textrm{4,5} \\ \textrm{Pour le dioxyde de carbone} &\mathbf{n_i-n_{i,0}}=(+1)\times\textrm{0,5}+(+2)\times\textrm{1,0}=+\textrm{2,5}\\ \textrm{Pour l'eau} & \mathbf{n_i-n_{i,0}}=(+2)\times\textrm{0,5}+(+3)\times\textrm{1,0}=+\textrm{4,0} \end{array}}\)

Exemple : L'avancement de la réaction étant une grandeur extensive, sa valeur dépend de l'écriture de l'équation bilan.

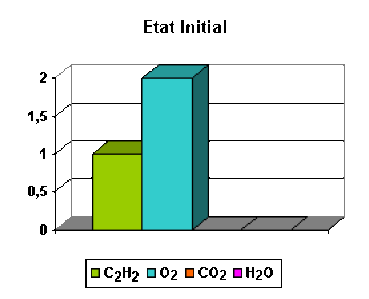
Considérons par exemple un mélange composé d'une mole d'acétylène et deux moles de dioxygène.

Calculons l'avancement de la réaction lorsque la réaction est terminée.

L'équation bilan de la réaction peut s'écrire :

\(\mathbf{(1) \textrm C_2\textrm H_2 + \frac{5}{2}. \textrm O_2 = 2. \textrm{CO}_2 + \textrm H_2\textrm O}\)

Mais on peut aussi l'écrire :

\(\mathbf{(2) 2. \textrm C_2\textrm H_2 + 5. \textrm O_2 = 4. \textrm{CO}_2 + 2. \textrm H_2\textrm O}\)

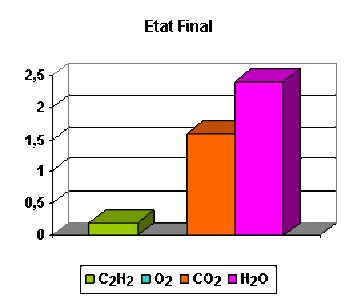
Calculons l'avancement de la réaction lorsque la réaction est terminée.

Avec l'équation (1), on trouve : \(\xi_1 = \textrm{0,8 mole}\)

Avec l'équation (2), on trouve : \(\xi_2 = \textrm{0,4 mole}\)

Pour calculer l'avancement \(\xi\) il nous faut connaître les quantités transformées de chaque substance. Ces quantités ne dépendent évidemment pas de l'écriture de l'équation bilan. Mais il n'en est pas de même pour l'avancement \(\xi\) puisque, pour une même substance, les coefficients stoechiométriques sont différents dans les deux équations. Essayez de retrouver par vous-même les valeurs de \(\xi_1\) et \(\xi_2\) .

Pour calculer l'avancement il faut d'abord déterminer les quantités transformées de chaque substance. On trouve les quantités transformées suivantes :

	C₂H₂	O₂	CO₂	H ₂O
n_i - n_i,0	- 0,8	- 2,0	+ 1,6	+ 0,8

Si vous voulez des détails sur ces calculs des quantités transformées cliquez ici^[3].

Les quantités de substances transformées (donc les quantités restantes) ne dépendent pas de la manière dont on a écrit l'équation bilan. Mais il n'en est pas de même pour l'avancement de la réaction, car les coefficients stoechiométriques pour chaque substance sont différents dans les deux équations !

Reprenons le tableau des quantités de substances transformées :

	C₂H₂	O₂	CO₂	H ₂O
n_i - n_i,0	- 0,8	- 2,0	+ 1,6	+ 0,8

Calculez l'avancement de la réaction en utilisant l'équation bilan :

\(\mathbf{(1) \textrm C_2\textrm H_2 + \frac{5}{2}. \textrm O_2 = 2. \textrm{CO}_2 + \textrm H_2\textrm O}\)

Reprenez maintenant le calcul avec l'équation :

\(\mathbf{(2) 2. \textrm C_2\textrm H_2 + 5. \textrm O_2 = 4. \textrm{CO}_2 + 2. \textrm H_2\textrm O}\)

Cliquez ici^[4] pour les résultats. On trouve \(\xi_1 = \textrm{0,8 mole}\) avec l'équation (1) et \(\xi_2 = \textrm{0,4 mole}\) avec l'équation (2). Vous voyez donc bien que, pour de mêmes quantités de matière transformées, la valeur de l'avancement de la réaction dépend de la manière dont on a écrit l'équation bilan. Cela est bien normal, puisque l'expression de l'avancement fait intervenir les coefficients stœchiométriques, lesquels dépendent de l'équation bilan.

En conclusion :

La valeur de l'avancement de réaction ne dépend pas du constituant choisi pour le calculer mais dépend de l'écriture de l'équation bilan. On ne peut donc pas dissocier la valeur de l'avancement de réaction de l'équation bilan ayant servi à la calculer.

Notes

Concepts fondamentaux - Avancement de la réaction
Calcul des avancements
CH4
C2H6
O2
CO2
H2O
ni,0
0,5
1,0
Excès
0,0
0,0
ni
0,0
0,0
Reste
2,5
4,0
ni - ni,0
-0,5
-1,0
-4,5
2,5
4,0
Pour calculer l'avancement d'une réaction, on doit utiliser un réactif ou un produit qui n'intervient que dans cette réaction. Pour la réaction
\(\mathbf{(1) \textrm{CH}_4 + 2. \textrm O_2 = \textrm{CO}_2 + 2. \textrm H_2\textrm O}\)
il s'agit du méthane.
D'où : \(\mathbf{\xi_1=\frac{n_i-n_{i,0}}{\nu_i}=\frac{0-\textrm{0,5}}{-1}=\textrm{0,5 mole}}\)
REMARQUE : si on utilisait les quantités totales des autres substances (\(\textrm O_2\), \(\textrm{CO}_2\) ou \(\textrm H_2\textrm O\)) on commettrait une erreur... car elles ne sont pas consommées ou produites par la seule réaction (1). C'est néanmoins possible à condition d'utiliser les quantités consommées ou produites par la seule réaction (1).
Ainsi, pour le dioxygène, la quantité consommée totale est de 4,5 moles. Mais seulement 1,0 mole est consommée par la réaction (1). Soit – 1 pour tenir compte du fait qu'il s'agit d'une quantité disparue.
D'où : \(\mathbf{\xi_1=\frac{n_i-n_{i,0}}{\nu_i}=\frac{-\textrm{1,0}}{-2}=\textrm{0,5 mole}}\)
On retrouve bien la même valeur qu'avec le méthane.
De la même façon, pour la réaction
\(\mathbf{(2) \textrm C_2\textrm H_6 + \frac{7}{2}. \textrm O_2 = 2. \textrm{CO}_2 + 3. \textrm H_2\textrm O}\)
en se référant à l'éthane, on trouve :
D'où : \(\mathbf{\xi_2=\frac{n_i-n_{i,0}}{\nu_i}=\frac{0-\textrm{1,0}}{-1}=\frac{-\textrm{1,0}}{-1}=\textrm{1,0 mole}}\)
REMARQUE : on retrouverait le même résultat en utilisant les quantités des autres substances consommées ou produites par la seule réaction (2).
Ainsi pour le dioxygène, la quantité consommée totale est de 4,5 moles. Mais seulement 3,5 moles sont consommées par la réaction (2).
Soient – 3,5 pour tenir compte du fait qu'il s'agit d'une quantité disparue.
D'où : \(\mathbf{\xi_1=\frac{n_i-n_{i,0}}{\nu_i}=\frac{-\textrm{3,5}}{-7/2}=\textrm{1,0 mole}}\)
On retrouve bien la même valeur qu'avec l'éthane.
A retenir : Pour calculer l'avancement d'une réaction, on doit utiliser un réactif ou un produit qui n'intervient que dans cette réaction. Si on se réfère à un réactif ou un produit intervenant dans plusieurs réactions, il faut utiliser les quantités consommées ou produites par le seul jeu de la réaction considérée.
Calcul des quantités transformées
On peut faire le calcul des quantités transformées indifféremment avec les deux équations bilan
\(\mathbf{(1) \textrm C_2\textrm H_2 + \frac{5}{2}. \textrm O_2 = 2. \textrm{CO}_2 + \textrm H_2\textrm O}\)
\(\mathbf{(2) 2. \textrm C_2\textrm H_2 + 5. \textrm O_2 = 4. \textrm{CO}_2 + 2. \textrm H_2\textrm O}\)
Faisons le calcul avec l'équation (1)
Les quantité initiales \(n_{\textrm C_2\textrm H_{2,0} = \textrm{1,0 mole}}\), \(n_{\textrm O_{2,0}} = \textrm{2,0 moles}\) ne sont pas dans les proportions stœchiométriques.
\(\mathbf{\frac{n_{\textrm C_2\textrm H_{2,0}}}{n_{\textrm O_{2,0}}}=\frac{\textrm{1,0}}{\textrm{2,0}}=\textrm{0,5}>\frac{\textrm v_{\textrm C_2\textrm H_2}}{\textrm v_{\textrm O_2}}=\frac{-1}{-5/2}=\textrm{0,4}}\)
Il y a un excès d'acétylène par rapport à la quantité de dioxygène disponible. Lorsque la réaction est terminée, tout le dioxygène sera consommé, d'où pour le dioxygène la quantité transformée \(n_i – n_{i,0} = 0 – 2 = -\textrm{2,0 mole}\). La quantité d'acétylène consommée se déduit de la quantité de dioxygène disponible :
\(\mathbf{\frac{\textrm C_2\textrm H_{2,\textrm{consommé}}}{-1}=\frac{\textrm O_{2,\textrm{consommé}}}{-2/5}}\)
D'où la quantité d'acétylène transformée = \(2/5 \times (–\textrm{2,0}) = – \textrm{0,8 moles}\). La quantité de dioxyde de carbone formée est le double de la quantité d'acétylène disparue soit \(2 \times \textrm{0,8} = \textrm{1,6 moles}\). La quantité d'eau formée est égale à la quantité d'acétylène disparue soit 0,8 mole.
Faisons maintenant le calcul avec l'équation (2)
\(\mathbf{(2) 2. \textrm C_2\textrm H_2 + 5. \textrm O_2 = 4. \textrm{CO}_2 + 2. \textrm H_2\textrm O}\)
Les quantité initiales \(n_{\textrm C_2\textrm H_{2,0} = \textrm{1,0 mole}}\) et \(n_{\textrm O_{2,0}} = \textrm{2,0 moles}\) ne sont pas dans les proportions stœchiométriques:
\(\mathbf{\frac{n_{\textrm C_2\textrm H_{2,0}}}{n_{\textrm O_{2,0}}}=\frac{\textrm{1,0}}{\textrm{2,0}}=\textrm{0,5}>\frac{\textrm v_{\textrm C_2\textrm H_2}}{\textrm v_{\textrm O_2}}=\frac{-2}{-5}=\textrm{0,4}}\)
Il y a donc un excès d'acétylène par rapport à la quantité de dioxygène disponible. Lorsque la réaction est terminée, tout le dioxygène sera consommé, d'où pour le dioxygène la quantité transformée \(n_i – n_{i,0} = 0 – 2 = -\textrm{2,0 mole}\). La quantité de butane consommée se déduit de la quantité de dioxygène :
\(\mathbf{\frac{\textrm C_2\textrm H_{2,\textrm{consommé}}}{-2}=\frac{\textrm O_{2,\textrm{consommé}}}{-5}}\)
D'où quantité d'acétylène transformée \(\mathbf{\xi=\frac{n_i-n_{i,0}}{\nu_i}=\frac{4}{2}=2}\)
La quantité de dioxyde de carbone formée est le double de la quantité d'acétylène disparue, soit \(2\times \textrm{0,8} = \textrm{1,6 moles}\). La quantité d'eau formée est le triple de de la quantité d'acétylène disparue, soit \(2 \times \textrm{0,8} = \textrm{2,4 moles}\).
Calcul de l'avancement
On peut faire le calcul de l'avancement de la réaction à partir de n'imprte quel composé d'une équation bilan
\(\mathbf{(1) \textrm C_2\textrm H_2 + \frac{5}{2}. \textrm O_2 = 2. \textrm{CO}_2 + \textrm H_2\textrm O}\)
\(\mathbf{(2) 2. \textrm C_2\textrm H_2 + 5. \textrm O_2 = 4. \textrm{CO}_2 + 2. \textrm H_2\textrm O}\)
Avec l'équation (1)
à partir de l'acétylène
\(\mathbf{\xi_1=\frac{n_i-n_{i,0}}{\nu_i}=\frac{-\textrm{0,8}}{-1}=\textrm{0,8 mole}}\)
à partir du dioxygène
\(\mathbf{\xi_1=\frac{n_i-n_{i,0}}{\nu_i}=\frac{-\textrm{2,0}}{-5/2}=\textrm{0,8 mole}}\)
à partir du dioxyde de carbone
\(\mathbf{\xi_1=\frac{n_i-n_{i,0}}{\nu_i}=\frac{\textrm{1,6}}{2}=\textrm{0,8 mole}}\)
à partir de l'eau
\(\mathbf{\xi_1=\frac{n_i-n_{i,0}}{\nu_i}=\frac{\textrm{0,8}}{1}=\textrm{0,8 mole}}\)
Avec l'équation (2)
à partir de l'acétylène
\(\mathbf{\xi_2=\frac{n_i-n_{i,0}}{\nu_i}=\frac{-\textrm{0,8}}{-2}=\textrm{0,4 mole}}\)
à partir du dioxygène
\(\mathbf{\xi_2=\frac{n_i-n_{i,0}}{\nu_i}=\frac{-\textrm{2,0}}{-5}=\textrm{0,4 mole}}\)
à partir du dioxyde de carbone
\(\mathbf{\xi_2=\frac{n_i-n_{i,0}}{\nu_i}=\frac{\textrm{1,6}}{4}=\textrm{0,4 mole}}\)
à partir de l'eau
\(\mathbf{\xi_2=\frac{n_i-n_{i,0}}{\nu_i}=\frac{\textrm{0,8}}{2}=\textrm{0,4 mole}}\)

	CH4	C2H6	O2	CO2	H2O
ni,0	0,5	1,0	Excès	0,0	0,0
ni	0,0	0,0	Reste	2,5	4,0
ni - ni,0	-0,5	-1,0	-4,5	2,5	4,0