Réactions élémentaires, mécanismes
Points de vue macroscopique et microscopique de la réaction
Dans ce qui précède, nous avons introduit la vitesse d'une réaction et les concepts qui en dérivent (loi de vitesse et ordre de réaction) à partir des variations des quantités de réactifs ou de produits observées au cours du temps. Autrement dit, nous nous sommes placés d'un point de vue macroscopique.
Du point de vue microscopique, la réaction se traduit à l'échelle des molécules par la rupture de certaines liaisons et l'établissement d'autres liaisons chimiques, entraînant la disparition des réactifs et la formation des produits.
Réaction élémentaire
Lorsqu'une réaction s'effectue simplement en une seule étape, faisant intervenir seulement les réactifs, on dit qu'il s'agit d'une réaction élémentaire.
Exemple :
La décomposition thermique du cyclobutane en phase gazeuse en deux molécules d'éthylène \(\mathbf{\textrm C_4\textrm H_8 = 2. \textrm C_2\textrm H_4}\) :
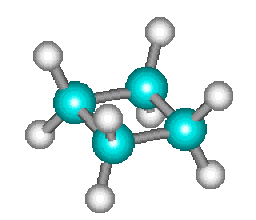
\(\mathbf=\)
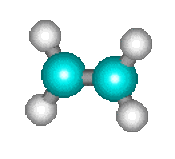
\(\mathbf+\)

s'effectue directement sans que l'on ait pu mettre en évidence d'étapes intermédiaires. On doit donc la considérer comme une réaction élémentaire.
Exemple :
La réaction \(\mathbf{\textrm{NO} + \textrm O_3 = \textrm{NO}_2 + \textrm O_2}\) s'effectue également en une seule étape au cours de laquelle il y a transfert direct d'un atome d'oxygène entre les molécules \(\textrm{NO}\) et \(\textrm O_3\).
Molécularité
On appelle molécularité le nombre d'entités chimiques (molécules, ions, radicaux) qui participent à une réaction élémentaire.
Exemple :
La décomposition du cyclobutane, vue ci-dessus, fait intervenir une seule molécule de cyclobutane lors de la décomposition. La molécularité est égale à un. La réaction est dite monomoléculaire.
Par contre, dans le deuxième exemple, \(\mathbf{\textrm{NO} + \textrm O_3 = \textrm{NO}_2 + \textrm O_2}\), il y a participation de deux molécules dans la réaction élémentaire. On dira que la molécularité est égale à deux. On parle alors de réaction bimoléculaire.
Les réactions élémentaires bimoléculaires sont les plus fréquentes. Les réactions monomoléculaires le sont moins. Les réactions trimoléculaires sont beaucoup plus rares, car elles ne peuvent se produire que lors de la rencontre simultanée de trois entités, ce qui est statistiquement très improbable. On ne connaît pas de réaction élémentaire de molécularité supérieure à trois.
Ordre et molécularité
Nous avons vu que la loi de vitesse d'une réaction est établie expérimentalement à partir des mesures d'évolution des quantités des réactifs en fonction du temps. Il s'agit donc d'une expression empirique qui traduit l'évolution macroscopique du système chimique.
Lorsque la loi de vitesse prend la forme simple d'un monôme en fonction des concentrations, on dit que la réaction admet un ordre. On appelle ordre partiel de la réaction par rapport à un réactif la puissance qui affecte la concentration de ce réactif dans l'expression de la loi de vitesse.
Vous pouvez revoir à ce sujet la partie de ce chapitre traitant l' Ordre de réaction
Les ordres partiels ainsi déterminés ne sont pas nécessairement égaux aux coefficients stœchiométriques de la réaction considérée. Cependant, si on considère une réaction élémentaire, on connaît le nombre d'entités chimiques qui participent à l'acte réactionnel. Il est alors possible d'en déduire l'ordre de cette réaction élémentaire.
Par exemple, dans le cas d'une réaction bimoléculaire, il faut évidemment que les deux molécules se rencontrent (entrent en contact) pour que la réaction puisse se produire.Il est dès lors facile de comprendre que la vitesse de la réaction doit être proportionnelle à la fréquence des rencontres entre les deux sortes de molécules. Sans entrer dans le détail de la démonstration, on peut établir que la fréquence de ces chocs est elle-même proportionnelle à la concentration de chaque réactifs. Ainsi, pour une réaction se produisant simplement par contact entre deux molécules \(\textrm A\) et \(\textrm B\), la vitesse de la réaction doit être de la forme :
\(\mathbf{\textrm v=k.C_\textrm A.C_\textrm B}\)
\(C_\textrm A\) et \(C_\textrm B\) étant les concentration en \(\textrm A\) et \(\textrm B\).
La réaction sera donc d'ordre global 2. Dans ce cas, l'ordre de la réaction est égal à la molécularité de la réaction élémentaire.
Le raisonnement que nous venons de tenir pour une réaction bimoléculaire s'applique également aux réactions élémentaires monomoléculaires ou trimoléculaires.
Règle :
On en conclut de manière générale : dans le cas d'une réaction élémentaire, l'ordre global est égal au nombre de molécules qui entrent en contact (molécularité). De plus, les ordres partiels sont égaux au nombre de molécules de chaque espèce qui interviennent dans l'acte réactionnel.
Ainsi, la réaction de décomposition du cyclobutane qui comme nous l'avons vu est une réaction élémentaire, suit une loi de vitesse d'ordre 1.
Réactions complexes
Lors de l'étude d'une nouvelle réaction, nous ne savons pas si elle s'effectue en une seule étape simple ou si au contraire elle se déroule en faisant intervenir plusieurs autres réactions. Autrement dit, rien ne nous indique a priori s'il s'agit d'une réaction élémentaire ou pas. Dans certains cas, il est facile de se rendre compte que la réaction ne peut pas être une réaction élémentaire.
C'est le cas des réactions qui font intervenir de nombreuses entités (trois ou plus), la réaction n'est certainement pas élémentaire car nous savons que les chocs tri moléculaires sont extrêmement rares et que les réactions de molécularité supérieure à trois ne sont pas envisageables.
Exemple :
L'équation bilan de l'oxydation des ions \(\textrm{Fe}^{2+}\) par l'ion permanganate s'écrit :
\(\mathbf{\textrm{MnO}_4^- + 5. \textrm{Fe}^{2+} + 8. \textrm H_3\textrm O^+ = \textrm{Mn}^{2+} + 5. \textrm{Fe}^{3+} + 12. \textrm H_2\textrm O}\)
Il n'est pas possible d'imaginer que la réaction puisse s'effectuer en une seule étape au cours de laquelle les 5 ions \(\textrm{Fe}^{2+}\) rencontreraient les 8 ions \(\textrm H_3\textrm O^+\) et l'ion \(\textrm{MnO}_4^-\) ce qui ferait un ensemble de 14 entités chimiques devant se trouver au même endroit, au même instant !
Une telle réaction se déroule donc forcément par une suite d'étapes plus simples. L'ensemble des étapes élémentaires qui concourent au déroulement d'une réaction est appelé mécanisme réactionnel.
Une autre situation correspond aux cas où la réaction n'admet pas d'ordre simple et obéit à une loi de vitesse compliquée. On peut alors conclure que la réaction n'est pas une réaction élémentaire. En effet, si elle l'était, on devrait observer un ordre observé égal à la molécularité.
Exemple :
La réaction \(\mathbf{\textrm H_2 + \textrm{Br}_2 = 2. \textrm{HBr}}\) obéit à la loi de vitesse :
\(\textrm v=k.\frac{C_{\textrm H_2}.C_{\textrm{Br}_2}^{1/2}}{1+K.\frac{C_\textrm{HBr}}{C_{\textrm{Br}_2}}}\)
On peut donc être certain qu'il ne s'agit pas d'une réaction élémentaire car, si c'était le cas, la loi de vitesse devrait être du premier ordre par rapport à chaque réactif.
Si la réaction admet un ordre simple, mais que celui ci ne correspond pas à sa stœchiométrie, on peut également conclure que la réaction n'est pas élémentaire.
Exemple :
la réaction de décomposition en phase gazeuse de \(\textrm N_2\textrm O_5\) :
\(\mathbf{2.\textrm N_2\textrm O_5=4.\textrm{NO}_2+\textrm O_2}\)
obéit à une loi du premier ordre. La réaction, telle qu'elle est écrite, n'est donc pas une réaction élémentaire bimoléculaire, car si elle l'était la loi de vitesse devrait être du second ordre.
Notez qu'en considérant l'équation bilan ci-dessus, on pourrait formellement diviser tous les coefficients par 2 et écrire :
\(\mathbf{\textrm N_2\textrm O_5 = 2. \textrm{NO}_2 +\frac{1}{2}. \textrm O_2}\)
Mais une telle écriture n'est pas acceptable pour une étape élémentaire, car elle fait intervenir un coefficient fractionnaire. Or, au niveau moléculaire, on ne peut pas considérer des demi molécules !
Reste le cas de réactions qui obéissent à un ordre simple égal à leur molécularité.
Exemple :
La réaction \(\mathbf{\textrm H_2 + \textrm I_2 = 2. \textrm{HI}}\) obéit à la loi de vitesse : \(\textrm v = k. C_{\textrm H_2}. C_{\textrm I_2}\)
Les ordres partiels sont égaux aux coefficients stœchiométriques.
Il se peut donc que la réaction soit une réaction élémentaire, mais cela n'est pas certain pour autant !
Effectivement, on a longtemps considéré cette réaction comme un exemple de réaction élémentaire bimoléculaire.En fait des études plus fines de la variation du coefficient de vitesse avec la température ont montré, qu'au- dessus d'une température de l'ordre de 600 K il convenait de tenir compte d'une étape faisant intervenir une collision entre un atome d'iode et une molécule de dihydrogène. Cette observation oblige à prendre en compte une étape de formation des atomes d'iode à partir de la molécule de diiode.
Mécanisme
On appelle mécanisme l'ensemble des réactions élémentaires qui rendent compte convenablement du déroulement d'une réaction. Un mécanisme est donc une hypothèse qui doit être conforme à l'ensemble des observations expérimentales disponibles. En particulier, un mécanisme doit traduire correctement la stœchiométrie de la réaction et être compatible avec la loi de vitesse déterminée expérimentalement.
Parfois, on peut proposer plusieurs mécanismes qui soient compatibles avec l'ensemble des observations expérimentales. On cherchera alors à concevoir des expériences nouvelles, ou à mettre au point de nouvelles méthodes d'investigation pour trancher entre ces mécanismes. Mais, même si un seul mécanisme reste compatible avec l'ensemble des données expérimentales, il doit toujours être considéré comme une hypothèse.
D'un point de vue méthodologique, une hypothèse (et plus généralement une théorie scientifique) est donc toujours "en sursis", elle ne reste acceptable que tant qu'elle n'a pas été contredite (on dit "falsifiée") par de nouvelles observations. Il importe donc de bien comprendre qu'on ne peut jamais prouver qu'une hypothèse ou une théorie soit juste. On peut seulement fixer son domaine de validité et la précision avec laquelle elle rend compte des observations.